2022-2023学年吉林省长春市东北师大附中高一（下）期末数学试卷

一、单项选择题（本题共8小题，每小题4分，共32分.在每小题给出的四个选项中，只有一项是符合题目要求的）

• 1．已知（1-i）z=6，则z=（　　）

  A．-3-i

  B．3-i

  C．-3+3i

  D．3+3i
  组卷：17引用：2难度：0.8

  解析

• 2．已知向量

  a

  =

  （

  2

  ，

  1

  ）

  ，

  b

  =

  （

  m

  ,-

  1

  ）

  ，若

  （

  a

  -

  b

  ）

  ⊥

  a

  ，则实数m=（　　）

  A．3

  B．-3

  C．4

  D．-4
  组卷：25引用：1难度：0.8

  解析

• 3．已知△ABC的内角A，B，C的对边分别是a,b,c,a=16，b=8，A=60°，则cosB=（　　）

  A． - 3 4

  B． 3 4

  C． - 13 4

  D． 13 4
  组卷：283引用：4难度：0.8

  解析

• 4．已知两条直线l,m与两个平面α，β，下列命题正确的是（　　）

  A．若l∥α，l⊥m,则m⊥α	B．若l⊥α，l∥β，则α⊥β
  C．若l∥α，m∥α，则l∥m	D．若α∥β，m∥α，则m∥β
  组卷：514引用：5难度：0.8

  解析

• 5．2023年吉林省高考分数公布后，附中再续辉煌，高三一班平均分657分，其中的12名同学成绩分别是（单位：分）：673，673，677，679，682，682，684，685，687，691，697，705，则这12名学生成绩的第75百分位数是（　　）

  A．689

  B．687

  C．679

  D．678
  组卷：14引用：1难度：0.7

  解析

• 6．在边长为2的正三角形ABC中，

  AD

  =

  1

  3

  DB

  ，

  CE

  =

  EB

  ，则

  AE

  •

  DE

  =（　　）

  A．- 9 4

  B． 3 2

  C．- 3 2

  D． 9 4
  组卷：166引用：3难度：0.7

  解析

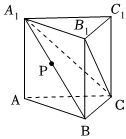• 7．《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为堑堵，在堑堵ABC-A₁B₁C₁中，若AB=BC=AA₁=4，若P为线段BA₁中点，则点P到平面A₁B₁C的距离为（　　）

  A．1

  B． 2 2

  C． 2

  D．4
  组卷：40引用：1难度：0.5

  解析

四、解答题：本题共6小题。共56分、解答应写出文字说明、证明过程或演算步骤.

• 21．已知在锐角△ABC中，内角A，B，C所对的边分别为a,b,c,

  2

  c

  -

  a

  =

  3

  bsin

  C

  -

  bcos

  C

  ．
  （1）求角B；
  （2）若

  b

  =

  2

  3

  ，D为AC的中点，求线段BD长度的取值范围．
  组卷：68引用：1难度：0.6

  解析

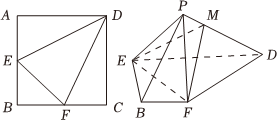• 22．如图，在正方形ABCD中，点E、F分别为AB、BC的中点，将△AED，△DCF分别沿DE、DF折起，使A，C两点重合于P，连接EF，PB．
  （1）点M是PD上一点．若PB∥平面EFM，则

  PM

  MD

  为何值？并说明理由；
  （2）点M是PD上一点，若MD=3PM，求二面角M-EF-D的余弦值．
  组卷：167引用：4难度：0.6

  解析