当前位置：试卷中心 > 试卷详情

2022-2023学年湖北省武汉六中高一（下）第六次月考数学试卷

发布：2024/5/24 8:0:9

一、选择题（本大题共8小题，每小题5分，共40分，每个小题只有一个正确选项）

1．若
（
i
+
z
）
z
=
4
+
2
i
，则
z
+
z
2
=（　　）
A．-2 B．0 C．1 D．2
组卷：18引用：3难度：0.8
解析
2．对于平面α和共面的直线m、n,下列命题中真命题是（　　）
A．若m⊥α，m⊥n,则n∥α
B．若m∥α，n∥α，则m∥n
C．若m⊂α，n∥α，则m∥n
D．若m、n与α所成的角相等，则m∥n
组卷：267引用：35难度：0.9
解析
3．已知直线m、n和平面α、β满足m⊥n,m⊥α，α⊥β，则（　　）
A．n⊥β B．n∥β，或n⊂β C．n⊥α D．n∥α，或n⊂α
组卷：996引用：19难度：0.7
解析
4．在梯形ABCD中，AC，BD交于点O，
3
BC
=
4
AD
，则
DC
=（　　）
A．
3
4
OB
+
OC
B．
3
4
OB
-
OC
C．
OB
+
3
4
OC
D．
OB
-
3
4
OC
组卷：69引用：3难度：0.7
解析
5．设A，B，C，D是球面上的四个点，且在同一平面内，AB=BC=CD=DA=3，球心到该平面的距离是球半径的一半，则球的体积是（　　）
A．
8
6
π
B．
64
6
π
C．
24
2
π
D．
72
2
π
组卷：690引用：4难度：0.7
解析
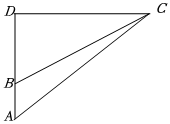6．火箭造桥技术是我国首创在陡峭山区建桥的一种方法．由两枚火箭牵引两条足够长的绳索精准的射入对岸的指定位置，是建造高空悬索桥的关键．位于湖北省的四渡河大桥就是首次用这种技术建造的悬索桥．工程师们需要测算火箭携带的引导索的长度（引导索比较重，如果过长影响火箭发射），已知工程师们在建桥处C看对岸目标点D的正下方地面上一标志物AB的高为h,从点C处看点A和点B俯角为α，β．求一枚火箭应至少携带引导索CD的长度（　　）
A．
hsinαcosβ
sin
（
α
-
β
）
B．
hcosαcosβ
sinβ
C．
hcosαcosβ
sin
（
α
-
β
）
D．
hcosαsinβ
cosβ
组卷：64引用：3难度：0.6
解析
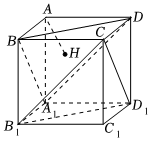7．如图，正方体AC₁的棱长为1，过点A作平面A₁BD的垂线，垂足为点H，则以下命题中，错误的命题是（　　）
A．点H是△A₁BD的垂心
B．AH垂直平面CB₁D₁
C．AH的延长线经过点C₁
D．直线AH和BB₁所成角为45°
组卷：315引用：29难度：0.9
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6小题，共70分，解答须写出必要的文字说明、证明过程或演算步骤）

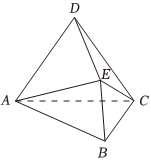21．如图，在多面体ABCDE中，平面ACD⊥平面ABC，BE⊥平面ABC，△ABC和△ACD均为正三角形，AC=4，BE=
3
．
（1）在线段AC上是否存在点F，使得BF∥平面ADE？如果存在，求出AF的值；如果不存在说明理由；
（2）求平面CDE与平面ABC所成的锐二面角的正切值．
组卷：32引用：1难度：0.5
解析
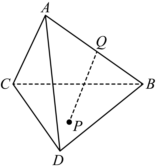22．如图，在三棱锥A-BCD中，∠ABC=45°，点P在平面BCD内，点Q在AB上，且满足PQ⊥AB．
（1）过Q作AB的垂面QEF，交平面BCD于EF，过B作BM⊥EF交CD于点M，证明：EF⊥AM；
（2）当PQ与平面BCD所成最大角的正切值是
15
3
时，求此时PQ与平面ABC所成角的余弦值．
组卷：48引用：4难度：0.5
解析