当前位置：试卷中心 > 试卷详情

2023-2024学年江西省宜春市铜鼓中学高二（上）周练数学试卷（四）（9月份）

发布：2024/9/28 9:0:1

一、单项选择题（本大题共9小题，每题5分，共40分）

1．抛物线
y
=
3
4
x
2
的准线方程是（　　）
A．
y
=
-
1
3
B．
y
=
1
3
C．
y
=
-
2
3
D．
y
=
2
3
组卷：45引用：3难度：0.7
解析
2．倾斜角为120°的直线经过点（2，
3
）和（3，a），则a=（　　）
A．0 B．2
3
C．
2
3
3
D．
4
3
3
组卷：134引用：4难度：0.7
解析
3．已知空间向量
a
=
（
2
，
1
，-
3
）
，
b
=
（
-
1
，
2
，
3
）
，
c
=
（
7
，
6
，
z
）
，若三向量
a
、
b
、
c
共面，则实数z=（　　）
A．1 B．-9 C．-3 D．-1
组卷：316引用：6难度：0.5
解析
4．已知直线l₁：ax+y+3=0与l₂：2x+（a-1）y+a+1=0平行，则a=（　　）
A．-1或2 B．1或-2 C．-1 D．1
组卷：143引用：3难度：0.7
解析
5．已知F₁，F₂分别是双曲线
x
2
25
-
y
2
24
=
1
的左右焦点，点P在该双曲线上，若|PF₁|=11，则|PF₂|=（　　）
A．1或21 B．14或36 C．2 D．21
组卷：9引用：2难度：0.5
解析
6．若圆C₁：（x-1）²+y²=1与圆C₂：x²+y²-8x+8y+m=0相切，则m的值可以是（　　）
A．16或-4 B．7或-7 C．7或-4 D．16或-7
组卷：33引用：4难度：0.8
解析
7．设P是抛物线C₁：x²=4y上的动点，M是圆C₂：（x-5）²+（y+4）²=4上的动点，d是点P到直线y=-2的距离，那么d+|PM|的最小值是（　　）
A．
5
2
-2 B．
5
2
-1 C．
5
2
D．
5
2
+1
组卷：234引用：7难度：0.6
解析
8．设F₁，F₂是双曲线E：
x
2
a
2
-
y
2
b
2
=
1
（
a
＞
0
，
b
＞
0
）
的两个焦点，双曲线E与以O为圆心OF₁为半径的圆在第一象限的交点为P，且
|
P
F
1
|
=
3
2
|
P
F
2
|
，则该双曲线的离心率为（　　）
A．
13
2
B．
13
2
C．13 D．
13
组卷：239引用：2难度：0.6
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题（本大题共6题，共70分）

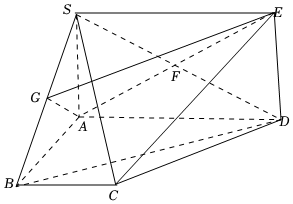25．如图，已知SA垂直于梯形ABCD所在的平面，矩形SADE的对角线交于点F，G为SB的中点，
∠
ABC
=∠
BAD
=
π
2
，
SA
=
AB
=
BC
=
1
2
AD
=
1
．
（1）求证：BD∥平面AEG；
（2）求二面角C-SD-E的余弦值；
（3）在线段EG上是否存在一点H，使得BH与平面SCD所成角的大小为
π
6
？若存在，求出GH的长；若不存在，说明理由．
组卷：265引用：8难度：0.4
解析
26．在平面直角坐标系xOy中，动圆P与圆
C
1
：
x
2
+
y
2
+
2
x
-
45
4
=
0
内切，且与圆C₂：
x
2
+
y
2
-
2
x
+
3
4
=
0
外切，记动圆P的圆心的轨迹为E．
（1）求轨迹E的方程；
（2）过椭圆C右焦点的直线l交椭圆于A，B两点，交直线x=4于点D．设直线QA，QD，QB的斜率分别为k₁，k₂，k₃，若k₂≠0，证明：
k
1
+
k
3
k
2
为定值．
组卷：89引用：5难度：0.5
解析