2022-2023学年浙江省宁波市镇海区中兴中学八年级（上）期中数学试卷

一、选择题（每小题4分，共40分）

• 1．下面四个图形分别是节能、节水、低碳和绿色食品标志，是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：5281引用：189难度：0.9

  解析

• 2．能说明命题“若x²≥4，则x≥2”为假命题的一个反例可以是（　　）

  A．x=-1

  B．x=2

  C．x=-3

  D．x=5
  组卷：369引用：13难度：0.6

  解析

• 3．下列长度的三条线段能组成三角形的是（　　）

  A．1，2，1

  B．2，3，6

  C．6，8，11

  D．1.5，2.5，4
  组卷：233引用：8难度：0.7

  解析

• 4．若x＞y,则下列式子错误的是（　　）

  A．x-2＞y-2

  B． x 3 ＞ y 3

  C．-x＜-y

  D．1-x＞1-y
  组卷：435引用：10难度：0.8

  解析

• 5．不等式组

  x - 5 ≤ 0

  x + 1 ＞ 0

  的解集在数轴上表示为（　　）

  A．

  B．

  C．

  D．
  组卷：215引用：7难度：0.6

  解析

• 6．已知一个等腰三角形的周长为20．若其中一边的长为4，则这个等腰三角形的腰长为（　　）

  A．4

  B．8

  C．4或8

  D．4或12
  组卷：128引用：3难度：0.6

  解析

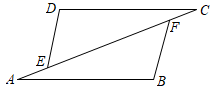• 7．如图，在△DEC和△BFA中，点A，E，F，C在同一直线上，已知AB∥CD，且AB=CD，若利用“ASA”证明△DEC≌△BFA，则需添加的条件是（　　）

  A．EC=FA

  B．∠A=∠C

  C．∠D=∠B

  D．BF=DE
  组卷：402引用：5难度：0.5

  解析

• 8．已知关于x的不等式组

  4 - 2 x ≥ 0

  1 2 x - a ＞ 0

  恰有4个整数解，则a的取值范围是（　　）

  A．-1＜a＜- 1 2

  B．-1≤a≤- 1 2

  C．-1＜a≤- 1 2

  D．-1≤a＜- 1 2
  组卷：3893引用：8难度：0.6

  解析

三、解答题（本大题有8小题，共80分）

• 23．定义：若a,b,c是△ABC的三边，且a²+b²=2c²，则称△ABC为“方倍三角形”．
  （1）对于①等边三角形②直角三角形，下列说法一定正确的是

  ．
  A．①一定是“方倍三角形”
  B．②一定是“方倍三角形”
  C．①②都一定是“方倍三角形”
  D．①②都一定不是“方倍三角形”
  （2）若Rt△ABC是“方倍三角形”，且斜边AB=

  3

  ，则该三角形的面积为

  ；
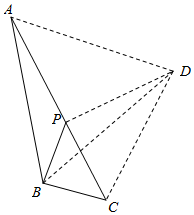
  （3）如图，△ABC中，∠ABC=120°，∠ACB=45°，P为AC边上一点，将△ABP沿直线BP进行折叠，点A落在点D处，连接CD，AD．若△ABD为“方倍三角形”，且AP=

  2

  ，求△PDC的面积．
  组卷：856引用：4难度：0.3

  解析

• 24．如图1，在等边△ABC中，线段AM为BC边上的高线．动点D在线段AM（点D与点A重合除外）上时，以CD为一边且在CD的下方作等边△CDE，连结BE．
  
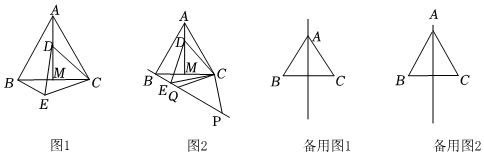
  （1）若DM=MC，则∠ACD=

  度，∠BCE=

  度；
  （2）判断AD与BE是否相等，请说明理由；
  （3）如图2，若AB=12，P、Q两点在直线BE上且满足CP=CQ=10，试求PQ的长．
  （4）在第（3）小题的条件下，当点D在线段AM的延长线（或反向延长线）上时，判断PQ的长是否为定值，若是，请直接写出PQ的长；若不是，请简单说明理由．
  组卷：284引用：3难度：0.3

  解析