2023-2024学年山东省烟台市芝罘区七年级(上)期中数学试卷(五四学制)
发布:2024/10/2 6:0:2
一、选择题。(每题3分,满分36分)
-
1.下列体育项目的示意图是轴对称图形的是( )
组卷:15引用:1难度:0.9 -
2.已知一个三角形的两边长分别为2和5,则这个三角形第三边的长可能是( )
组卷:24引用:2难度:0.6 -
3.如图,用三角尺作△ABC的边AB上的高,下列三角尺的摆放位置正确的是( )
组卷:405引用:15难度:0.5 -
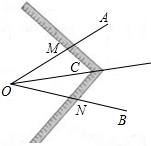 4.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )组卷:2306引用:60难度:0.7
4.工人师傅常用角尺平分一个任意角,做法如下:如图,∠AOB是一个任意角,在边OA、OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M、N重合,过角尺顶点C作射线OC,由此作法便可得△NOC≌△MOC,其依据是( )组卷:2306引用:60难度:0.7 -
 5.如图,将三角形纸片ABC沿直线DE折叠后,使得点B与点A重合,折痕分别交BC,AB于点D,E.如果AC=5cm,△ADC的周长为17cm,那么BC的长为( )组卷:293引用:21难度:0.9
5.如图,将三角形纸片ABC沿直线DE折叠后,使得点B与点A重合,折痕分别交BC,AB于点D,E.如果AC=5cm,△ADC的周长为17cm,那么BC的长为( )组卷:293引用:21难度:0.9 -
 6.在平面镜里看到背后墙上正放的电子钟示数如图所示,这时的时间应是( )组卷:130引用:2难度:0.7
6.在平面镜里看到背后墙上正放的电子钟示数如图所示,这时的时间应是( )组卷:130引用:2难度:0.7 -
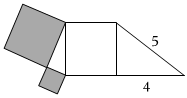 7.如图是由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是( )组卷:178引用:3难度:0.6
7.如图是由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是( )组卷:178引用:3难度:0.6 -
 8.如图,△ABC的中线BD、CE交于点O,四边形ADOE的面积是3,则△ABC的面积是( )组卷:198引用:6难度:0.5
8.如图,△ABC的中线BD、CE交于点O,四边形ADOE的面积是3,则△ABC的面积是( )组卷:198引用:6难度:0.5 -
 9.如图,△ABC中,AC=BC,∠C=40°,以点A为圆心、AB为半径的弧交BC、AC于D、E两点,连接AD、DE,则∠CDE的度数是( )组卷:101引用:3难度:0.7
9.如图,△ABC中,AC=BC,∠C=40°,以点A为圆心、AB为半径的弧交BC、AC于D、E两点,连接AD、DE,则∠CDE的度数是( )组卷:101引用:3难度:0.7
三、解答题。(共7小题,满分60分)
-
 26.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
26.如图,在△ABC中,AB=AC,D为CA延长线上一点,且DE⊥BC交AB于点F.
(1)求证:△ADF是等腰三角形;
(2)若AC=10,BE=3,F为AB中点,求DF的长.组卷:3440引用:9难度:0.5 -
27.阅读下面的证明过程:
如图1,△ACB、△ADC和△BEC都是直角三角形,其中AC=BC,且直角顶点都在直线l上,求证:△ACD≌△CBE.
证明:由题意,∠BCE+∠ACD=180°-90°=90°,∠DAC+∠ACD=90°.
∴∠DAC=∠BCE.
在△ACD和△CBE中,,∠ADC=∠CEB∠DAC=∠BCEAC=BC
∴△ACD≌△CBE.
像这种“在一条直线上有三个直角顶点”的几何图形,我们一般称其为“一线三垂直”图形,随着几何学习的深入,我们还将对这类图形有更深入的探索.
请结合以上阅读,解决下列问题:
(1)如图2,在△ABC中,∠BAC=90°,AB=AC,过点A作直线AE,BD⊥AE于点D,CE⊥AE于点E,探索BD、DE、CE之间的数量关系,并证明你的结论.
(2)如图3,△ABC和△ADE都是等腰直角三角形,∠ACB=∠AED=90°,AC=BC,AE=DE,且点E在BC上,连接BD,求证:∠ABD=90°.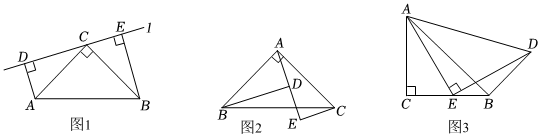
(3)如图4,在一款名为超级玛丽的游戏中,玛丽到达一个高为12米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为18米,高为4米的矮台B,请写出旗杆OM的高度是 .(不必书写解题过程)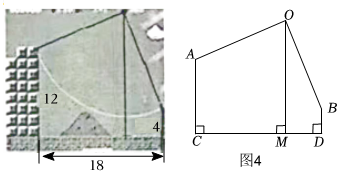 组卷:319引用:2难度:0.6
组卷:319引用:2难度:0.6


