2023-2024学年重庆市重点中学高二（上）月考数学试卷（10月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每个小题给出的四个选项中，只

• 1．若直线l经过原点和点A（-2，2），则它的斜率为（　　）

  A．-1

  B．1

  C．1或-1

  D．0
  组卷：16引用：2难度：0.9

  解析

• 2．在平行四边形ABCD中，A（1，-1，-3），B（2，2，4），C（0，3，6），则点D的坐标为（　　）

  A．（-1，3，3）

  B．（1，0，-1）

  C．（3，-1，2）

  D．（-1，0，-1）
  组卷：21引用：2难度：0.7

  解析

• 3．如果AB＞0，BC＞0，那么直线Ax-By-C=0不经过的象限是（　　）

  A．第一象限

  B．第二象限

  C．第三象限

  D．第四象限
  组卷：2445引用：45难度：0.9

  解析

• 4．已知直线l：（2m+1）x+（m+1）y+m=0经过定点P，直线l'经过点P，且l'的方向向量

  a

  =

  （

  3

  ，

  2

  ）

  ，则直线l'的方程为（　　）

  A．2x-3y+5=0

  B．2x-3y-5=0

  C．3x-2y+5=0

  D．3x-2y-5=0
  组卷：287引用：4难度：0.7

  解析

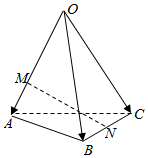• 5．如图，空间四边形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，点M在

  OA

  上，且OM=2MA，点N为BC中点，则

  MN

  =（　　）

  A． 1 2 a - 2 3 b + 1 2 c	B． - 2 3 a + 1 2 b + 1 2 c
  C． 1 2 a + 1 2 b - 1 2 c	D． 2 3 a + 2 3 b - 1 2 c
  组卷：2451引用：155难度：0.9

  解析

• 6．已知点A（-1，2），B（5，8），若过点C（1，0）的直线与线段AB相交，则该直线的斜率的取值范围是（　　）

  A．[-1，2]	B．（-∞，-1]∪[2，+∞）
  C．（-∞，-2]∪[1，+∞）	D．（-∞，-1）∪（2，+∞）
  组卷：41引用：3难度：0.7

  解析

• 7．设直线l的方程x+ycosθ+2=0，（θ∈R），则直线l的倾斜角α的取值范围是（　　）

  A．[0，π]	B．[ π 4 ， π 2 ]
  C．[ π 4 ， π 2 ）∪（ π 2 ， 3 π 4 ]	D．[ π 4 ， 3 π 4 ]
  组卷：144引用：5难度：0.9

  解析

四.解答题（17题10分，其余每题12分，共70分）

• 21．如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，三角形PAB为正三角形，且侧面PAB⊥底面ABCD．E，M 分别为线段AB，PD的中点．
  （1）求证：PB∥平面ACM；
  （2）在棱CD上是否存在点G，使平面GAM⊥平面ABCD，请说明理由．
  组卷：303引用：5难度：0.5

  解析

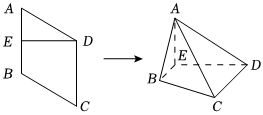• 22．如图，菱形ABCD的边长为2，∠BAD=60°，E为AB的中点．将△ADE沿DE折起，使A到达A'，连接A'B，A'C，得到四棱锥A'-BCDE．
  （1）证明：DE⊥A'B．
  （2）当二面角A'-DE-B在[

  π

  3

  ，

  2

  π

  3

  ]内变化时，求直线A'C与平面A'DE所成角的正弦的最大值．
  组卷：100引用：10难度：0.5

  解析