2023年山东省青岛市李沧区中考数学一模试卷

一、选择题（本大题共7小题，每小题3分，共24分）

• 1．随着电子技术的不断进步，电子元件的尺寸大幅度缩小，在芯片上某种电子元件大约只占有面积0.00000065mm²，0.00000065用科学记数法表示为（　　）

  A．6.5×107

  B．6.5×10-6

  C．6.5×10-8

  D．6.5×10-7
  组卷：2667引用：29难度：0.9

  解析

• 2．绝对值为

  1

  2023

  的数是（　　）

  A．-2023

  B． 1 2023

  C． - 1 2023

  D．± 1 2023
  组卷：321引用：2难度：0.8

  解析

• 3．如图是我国几家银行的标志，其中既是轴对称图形又是中心对称图形的有（　　）
  

  A．2个

  B．3个

  C．4个

  D．5个
  组卷：671引用：16难度：0.9

  解析

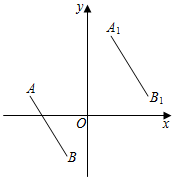• 4．如图，点A，B的坐标分别为（-3，1），（-1，-2），若将线段AB平移至A₁B₁的位置，点A₁，B₁的坐标分别为（a,4），（3，b），则a+b的值为（　　）

  A．2

  B．3

  C．4

  D．5
  组卷：614引用：3难度：0.5

  解析

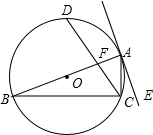• 5．如图，△ABC内接于⊙O，AB是⊙O的直径，直线AE是⊙O的切线，CD平分∠ACB，若∠CAE=21°，则∠BFC的度数为（　　）

  A．66°

  B．111°

  C．114°

  D．119°
  组卷：854引用：9难度：0.9

  解析

• 6．如图，过矩形ABCD的对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF，若AB=2

  3

  ，∠DCF=30°，则EF的长为（　　）

  A．4

  B．6

  C． 3

  D．2 3
  组卷：1258引用：8难度：0.7

  解析

• 7．用24块棱长分别为3cm,4cm,5cm的长方体积木搭成的大长方体表面积最小是（　　）

  A．808cm2

  B．900cm2

  C．960cm2

  D．768cm2
  组卷：257引用：1难度：0.5

  解析

二、选择题（本大题共2小题，每小题4分，共8分）下列每小题都给出标号为A、B、C、D的四个结论，其中有2-3个是正确的.每小题选对得4分；漏选得1分，不选、选错或选出的标号超过一个的不得分.

• 8．下列运算正确的有（　　）

  A．a2•a3=a5	B．a2+2a=3a3
  C．（a2）3=a5	D． 3 27 - （ 1 2 ） - 2 = - 1
  组卷：176引用：1难度：0.7

  解析

四、解答题（本大题共9小题，共66分）

• 24．如图①是我区的某蔬菜基地的种植棚，它一定意义上带动了我区的经济发展．其截面为图②所示的轴对称图形，点A，B在以O为顶点的抛物线上，BC⊥AB，AD⊥AB，BC=AD，点G在直线BC上，点E在直线AD上，FH∥AB．当以O为原点建立如图③所示的坐标系时，抛物线过点

  P

  （

  -

  2

  ，-

  1

  2

  ）

  ．
  （1）求抛物线的解析式．
  （2）若点O到地面距离为5米，记BC+AB+AD=p,当p最大时，求棚的跨度AB长．
  （3）在（2）的条件下，E点纵坐标为

  1

  -

  2

  ，F（2，1），为了使该棚更加牢固安全，需要把直线EF，GH向下平移到与抛物线相切的位置处焊接，求EF向下平移的距离．
  ​
  组卷：685引用：4难度：0.5

  解析

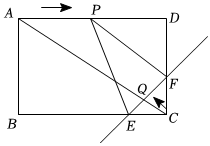• 25．已知矩形ABCD中，AC是对角线，AB=3cm,BC=4cm,点P为边AD上的一个动点，动点P从点A出发沿AD边向点D运动，速度是1cm/s,点Q为边C上的一个动点，动点Q从点C出发沿CA边向点A运动，速度是1cm/s,EF是过点Q的直线，分别交BC、CD于点E，F，且运动过程中始终保持EF⊥AC于Q；P、Q两点同时出发，设运动时间为t秒，且（0≤t≤

  9

  5

  ），解答下列问题：
  （1）连接PE，t为何值时，四边形ABEP是平行四边形？
  （2）连接EP、PF，设四边形PECF的面积为y cm²，求y关于t的函数关系式；
  （3）请从选择以下任意一题作答，我选

  （若同时作答①和②，按①解答计分）．
  ①连接BP，是否存在某一时刻t,使点E在∠BPD 平分线上时，若存在，求t的值，若不存在，请说明理由．
  ②是否存在某一时刻t,使点F在PE垂直平分线上，若存在，求t的值，若不存在，请说明理由．
  组卷：468引用：2难度：0.5

  解析