2022-2023学年湖北省孝感市八年级（下）期末数学试卷
发布：2024/6/29 8:0:10
一、精心选一选（本大题共8小题，每小题3分，满分24分，在每小题给出的四个选项中只有一个正确选项，请在答题卡上把正确答案的代号涂黑）
-
1．
=（ ）（2）2组卷：186引用：6难度：0.9 -
2．一组数据2，3，4，4，4，5，5的众数、中位数分别是（ ）
组卷：23引用：1难度：0.6 -
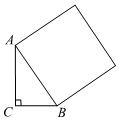3．如图，在△ABC中，∠C=90°，AC=3，BC=2，以AB为一条边向三角形外部作正方形，则正方形的面积是（ ）组卷：403引用：3难度：0.7 -
4．计算
的结果是（ ）（2+2）（2-2）组卷：45引用：1难度：0.5 -
5．若平行四边形中两个内角的度数比为1：3，则其中较大的内角是（ ）
组卷：145引用：3难度：0.6 -
6．若函数y=-2xm-2+n+1是正比例函数，则m+n（ ）
组卷：344引用：2难度：0.7 -
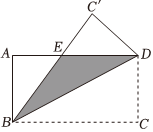7．如图，矩形ABCD中，AB=4cm,BC=8cm,如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积是（ ）组卷：95引用：3难度：0.5 -
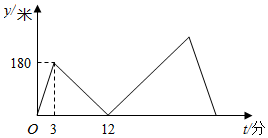8．甲、乙两人在笔直的人行道上同起点、同终点、同方向匀速步行1800米，先到终点的人原地休息．已知甲先出发3分钟，在整个步行过程中，甲、乙两人间的距离y（米）与甲出发后步行的时间t（分）之间的关系如图所示，下列结论：
①甲步行的速度为60米/分；
②乙走完全程用了22.5分钟；
③乙用9分钟追上甲；
④乙到达终点时，甲离终点还有270米．
其中正确的结论有（ ）组卷：1746引用：7难度：0.4
三、专心解一解（本大题共8小题，满分72分，请认真读题，冷静思考，解答题应写出必要的文字说明、证明过程或演算步骤，请把解题过程写在答题卡相应题号的位置）
-
23．问题背景：如图，已知四边形ABCD是正方形，点P是射线DC上一点，连接AP，在AP右侧以AP为边作正方形AEFP，连接BE，探究PC，CB，BE之间的数量关系．
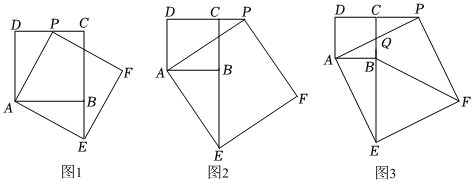
（1）问题发现：如图1，当点P在线段DC上时，PC，CB，BE之间的数量关系是 ；
（2）问题探究：如图2，当点P在DC的延长线上时，（1）中结论是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论，再给予证明；
（3）问题拓展：如图3，当点P在DC的延长线上时，设AP与BC交于点Q，若AD=2，BQ=QC，求BF的长．组卷：117引用：1难度：0.2 -
24．如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A的坐标为（-3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB交y轴于点H，连接BM．
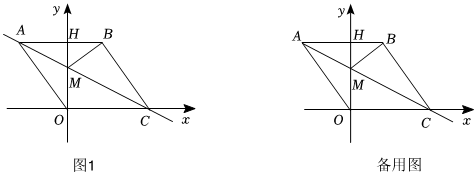
（1）菱形ABCO的边长是 ；
（2）求直线AC的解析式；
（3）动点P从点A出发，沿折线ABC方向以2个单位/秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t秒．
①求S与t之间的函数关系式；
②在点P运动过程中，当S=2，请直接写出t的值．组卷：192引用：2难度：0.3
