当前位置：试卷中心 > 试卷详情

2022-2023学年重庆市黔江区八年级（下）期末数学试卷

发布：2024/6/23 8:0:10

一、选择题：（共10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．

1．下列代数式①
1
x
，②
a
+
b
2
，③
a
π
，④
1
m
-
n
中，分式有（　　）
A．1个 B．2个 C．3个 D．4个
组卷：265引用：4难度：0.9
解析
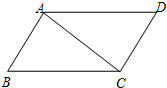2．如图，在▱ABCD中，∠BAC=68°，∠ACB=36°，则∠D等于（　　）
A．68° B．72° C．76° D．104°
组卷：63引用：4难度：0.5
解析
3．某课外学习小组有5人，在一次数学测验中的成绩分别是：120，100，135，100，125，则他们的成绩的中位数和众数分别是（　　）
A．120和135 B．120和100 C．116和100 D．135和100
组卷：220引用：3难度：0.8
解析
4．下列不能表示y是x的函数的是（　　）
A． B． C． D．
组卷：650引用：4难度：0.5
解析
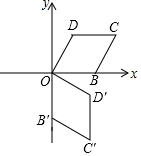5．如图，在菱形OBCD中，OB=1，相邻两内角之比为1：2，将菱形OBCD绕顶点O顺时针旋转90°，得到菱形OB′C′D′，则点C′的坐标为（　　）
A．（
3
2
，
3
2
） B．（
3
2
，-
3
2
） C．（
3
2
，-
3
2
） D．（
3
2
，
3
2
）
组卷：534引用：3难度：0.7
解析
6．在下列条件中，不能判定四边形为平行四边形的是（　　）
A．对角线互相平分
B．一组对边平行且相等
C．两组对边分别平行
D．一组对边平行，另一组对边相等
组卷：664引用：13难度：0.5
解析
7．将直线y=2x-3向右平移2个单位，再向上平移3个单位后，所得的直线的表达式为（　　）
A．y=2x-4 B．y=2x+4 C．y=2x+2 D．y=2x-2
组卷：7749引用：40难度：0.9
解析
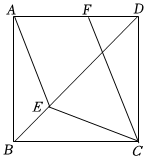8．如图，已知正方形ABCD中，DA=DE，CF∥AE，则∠ECF的度数是（　　）
A．30° B．35° C．40° D．45°
组卷：422引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题8个小题，第19题8分，20～26题每题10分，共78分）解答时每小题都必须写出必要的演算过程或推理步骤，请将解答过程书写在答题卡中对应的位置上.

25．在Rt△ABC中，∠ACB=90°，AC=4，BC=3，点P，Q分别从点A，点B同时出发，点P沿A→C→B以每秒1个单位长度速度运动，点Q以每秒
1
2
个单位长度的速度沿B→A运动，点P到达点B时点Q同时停止运动．点P的运动时间为t秒，△ABP的面积记为y₁，面积△AQC的记为y₂，回答下列问题：
（1）求出y₁，y₂与t之间的函数表达式并写出自变量的取值范围；
（2）在平面直角坐标系中画出y₁，y₂的图象，并写出函数y₁的一条性质；
（3）当y₁＜y₂时，直接写出t的取值范围．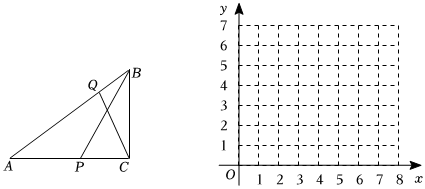
组卷：145引用：2难度：0.2
解析
26．如图①，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．
（1）连接MN，△BMN是等边三角形吗？为什么？
（2）求证：△AMB≌△ENB；
（3）①当M点在何处时，AM+CM的值最小；
②如图②，当M点在何处时，AM+BM+CM的值最小，请你画出图形，并说明理由．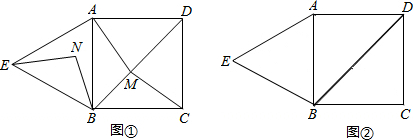
组卷：2860引用：10难度：0.3
解析