在Rt△ABC中，∠ACB=90°，AC=4，BC=3，点P，Q分别从点A，点B同时出发，点P沿A→C→B以每秒1个单位长度速度运动，点Q以每秒12个单位长度的速度沿B→A运动，点P到达点B时点Q同时停止运动．点P的运动时间为t秒，△ABP的面积记为y1，面积△AQC的记为y2，回答下列问题：
（1）求出y1，y2与t之间的函数表达式并写出自变量的取值范围；
（2）在平面直角坐标系中画出y1，y2的图象，并写出函数y1的一条性质；
（3）当y1＜y2时，直接写出t的取值范围．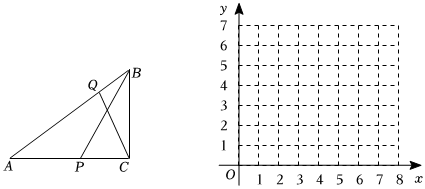
1
2
【考点】三角形综合题．
【答案】（1）y1=
；y2=•AQ•CH=（5-t）×=-t+6（0＜t＜7）；
（2）图象见解答；函数y1的性质：函数有最大值，最大值为6；
（3）当0＜t＜或＜t＜7时，y1＜y2．
3 2 t | （ 0 ＜ t ≤ 4 ） |
- 2 t + 14 | （ 4 ＜ t ＜ 7 ） |
1
2
1
2
1
2
12
5
3
5
（2）图象见解答；函数y1的性质：函数有最大值，最大值为6；
（3）当0＜t＜
20
7
40
7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/14 8:0:9组卷：145引用：2难度：0.2
相似题
-
1．已知等腰三角形ABC，∠F=2∠ABC，CD=kBD，∠FGC=α．
（1）如图1，当k=1时，
①探究DG与CE之间的数量关系；
②探究BE，CG与CE之间的关系（用含α的式子表示）．
（2）如图2，当k≠1时，探究BE，CG与CE之间的数量关系（用含k,α的式子表示）．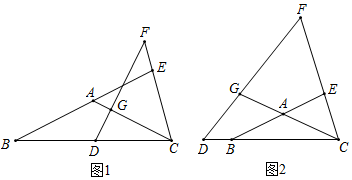
发布：2025/5/24 11:30:1组卷：343引用：3难度：0.2 -
2．已知：在△ABC中，AB=AC=10，BC=16，点P、D分别在射线CB、射线AC上，且满足∠APD=∠ABC．
（1）当点P在线段BC上时，如图1．
①如果CD=4.8，求BP的长；
②设B、P两点的距离为x,AP=y,求y关于x的函数关系式，并写出定义域．
（2）当BP=1时，求△CPD的面积．（直接写出结论，不必给出求解过程）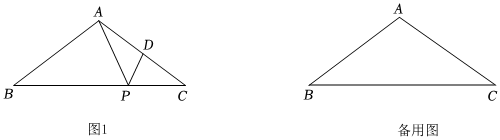
发布：2025/5/24 12:0:1组卷：310引用：1难度：0.1 -
3．如图，在△ABC中，∠A=α（0°＜α≤90°），将BC边绕点C逆时针旋转（180°-α）得到线段CD．
（1）判断∠B与∠ACD的数量关系并证明；
（2）将AC边绕点C顺时针旋转α得到线段CE，连接DE与AC边交于点M（不与点A，C重合）．
①用等式表示线段DM，EM之间的数量关系，并证明；
②若AB=a,AC=b,直接写出AM的长．（用含a,b的式子表示）发布：2025/5/24 14:0:2组卷：1301引用：9难度：0.2
