当前位置：试卷中心 > 试卷详情

2022-2023学年湖南师大附中高新实验中学七年级（下）期末数学试卷

发布：2024/7/15 8:0:9

一、选择题。（本大题共10小题，每小题3分，共30分）

1．64的平方根为（　　）
A．8 B．±8 C．-8 D．±4
组卷：1029引用：26难度：0.9
解析
2．已知a＞b,下列不等式中，不正确的是（　　）
A．a+4＞b+4 B．a-8＞b-8 C．5a＞5b D．-6a＞-6b
组卷：392引用：15难度：0.7
解析
3．下列调查统计中，适合做全面调查的是（　　）
A．了解格力空调的市场占有率
B．了解湖南卫视“歌手”节目的收视率
C．了解奔驰汽车每百公里耗油量
D．了解神舟飞船的设备零件的质量情况
组卷：64引用：2难度：0.9
解析
4．若一个三角形的两边长分别为3和7，则第三边长可能是（　　）
A．6 B．3 C．2 D．11
组卷：6380引用：57难度：0.7
解析
5．以下四种作△ABC边AC上的高，其中正确的作法是（　　）
A． B． C． D．
组卷：641引用：8难度：0.5
解析
6．如果多边形的每一个内角都是150°，那么这个多边形的边数是（　　）
A．8 B．10 C．12 D．16
组卷：960引用：13难度：0.6
解析
7．将含45°的直角三角板与直尺如图所示放置，有如下结论：
（1）∠1=∠2；（2）∠3=∠4；（3）∠2+∠3=90°；（4）∠3+∠5=180°，
其中正确的个数是（　　）
A．1个 B．2个 C．3个 D．4个
组卷：239引用：3难度：0.5
解析
8．在平面直角坐标系中，已知点A在第二象限，点A到x轴的距离为2，到y轴的距离为1，则点A的坐标为（　　）
A．（-2，1） B．（2，-1） C．（-1，2） D．（1，-2）
组卷：175引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题。（共9小题，17，18，19每小题6分，20，21每小题6分，22.23每小题6分，24.25每小题6分，共72分）

24．阅读理解：
定义：使方程（组）与不等式（组）同时成立的未知数的值称为此方程（组）和不等式（组）：的“理想解”，例如：已知方程2x-1=1与不等式x+1＞0，x=1当x=1时，2x-1=2×1-1=1，1+1=2＞0同时成立，则称“x=1”是方程2x-1=1与不等式x+1＞0的“理想解”．
问题解决：
（1）请判断方程3x-5=4的解是此方程与以下哪些不等式（组）的“理想解”
（直接填写序号）
①2x-3＞3x-1；
②2（x-1）≤4；
③
x
+
1
＞
0
x
-
2
≤
1
；
（2）若
x
=
m
y
=
n
是方程组
x
+
2
y
=
6
2
x
+
y
=
3
q
与不等式x+y＞1的“理想解”，求q的取值范围；
（3）当k＜3时，方程3（x-1）=k的解都是此方程与不等式4x+n＜x+2m的“理想解”，若m+n≥0且满足条件的整数n有且只有一个，求m的取值范围．
组卷：832引用：5难度：0.5
解析
25．在直角坐标系中，已知点A（a,0），B（b,c），C（d,0），且a是-8的立方根；方程2x^3b-5-3y^2b-2c+5=1是关于x、y的二元一次方程，d为不等式组
x
＞
b
x
＜
6
的最大整数解．

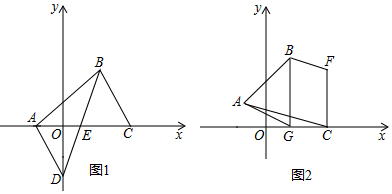
（1）求A、B、C的坐标；
（2）如图1，若D为y轴负半轴上的一个动点，连BD交x轴于点E，问是否存在点D，使得S_△ADE=S_△BCE？若存在，请求出点D的坐标；若不存在，请说明理由．
（3）如图2，若将线段AB向上平移2个单位长度，点G为x轴上一点，点F（5，n）为第一象限内一动点，连BF、CF、CA，若△ABG的面积等于由AB、BF、CF、AC四条线段围成图形的面积，求点G的横坐标（用含n的式子表示）．
组卷：1337引用：3难度：0.2
解析