2020-2021学年广东省茂名市高州市沙田一中七年级（下）期末数学试卷

一、选择题（本大题共10小题，每小题3分，共30分）

• 1．计算a²•a⁴的结果是（　　）

  A．a8

  B．a4

  C．a6

  D．a2
  组卷：364引用：35难度：0.9

  解析

• 2．2019年末，引发疫情的冠状病毒，被命名为COVID-19新型冠状病毒，冠状病毒的平均直径约是0.00000009米．数据0.00000009科学记数法表示为（　　）

  A．0.9×10-8

  B．9×10-8

  C．9×10-7

  D．0.9×10-7
  组卷：358引用：4难度：0.8

  解析

• 3．下列交通标志是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：5引用：2难度：0.9

  解析

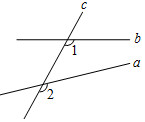• 4．如图，直线a,b被直线c所截，则∠1与∠2的位置关系是（　　）

  A．同位角

  B．内错角

  C．同旁内角

  D．邻补角
  组卷：1830引用：20难度：0.6

  解析

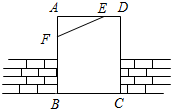• 5．如图，工人师傅砌门时，常用木条EF固定长方形门框ABCD，使其不变形，这样做的根据是（　　）

  A．三角形三个内角和等于180°

  B．直角三角形的两个锐角互余

  C．三角形具有稳定性

  D．两点之间，线段最短
  组卷：450引用：16难度：0.9

  解析

• 6．“任意买一张电影票，座位号是奇数”，此事件是（　　）

  A．不可能事件

  B．不确定事件

  C．必然事件

  D．确定事件
  组卷：100引用：5难度：0.9

  解析

• 7．下面每组数分别是三根小木棒的长度，它们能摆成三角形的是（　　）

  A．12cm,3cm,6cm	B．8cm,16cm,8cm
  C．6cm,6cm,13cm	D．2cm,3cm,4cm
  组卷：473引用：23难度：0.9

  解析

• 8．如图所示，货车匀速通过隧道（隧道长大于货车长）时，货车从进入隧道至离开隧道的时间x与货车在隧道内的长度y之间的关系用图象描述大致是（　　）
  

  A．

  B．

  C．

  D．
  组卷：588引用：10难度：0.7

  解析

五、解答题（三）（本大题2小题，毎小题10分，共20分）

• 24．如图，已知AB∥CD，现将一个直角△PMN放入图中，其中∠P=90°，PM交AB于点E，PN交CD于点F．
  
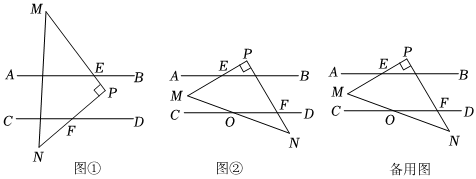
  （1）当△PMN所放位置如图①所示时，探索∠PFD与∠AEM的数量关系，并说明理由；
  （2）当△PMN所放位置如图②所示时，试探索∠PFD与∠AEM的数量关系（不需要说明理由）；
  （3）在（2）的条件下，若MN与CD交于点O，且∠DON=30°，∠PEB=15°，求∠N的度数．
  组卷：110引用：3难度：0.4

  解析

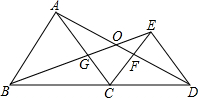• 25．如图，△ABC和△ECD都是等边三角形，B，C，D三点共线，AD 与BE相交于点O，AD与CE交于点F，AC与BE交于点G．
  （1）找出图中的一对全等三角形，并说明理由．
  （2）求∠BOD的度数．
  （3）连接GF，判断△CGF的形状，并说明理由．
  组卷：677引用：3难度：0.5

  解析