2022-2023学年吉林省长春市榆树市八号镇三校联考七年级（下）月考数学试卷（4月份）

一．选择题（共8小题，每题3分共24分）

• 1．下列方程中，是一元一次方程的是（　　）

  A．2x=5

  B．x+y=2

  C．x2-2x=1

  D．xy=2
  组卷：18引用：3难度：0.9

  解析

• 2．已知△ABC的三个内角度数比为2：3：4，则这个三角形是（　　）

  A．锐角三角形

  B．直角三角形

  C．钝角三角形

  D．无法确定
  组卷：83引用：5难度：0.6

  解析

• 3．下列正多边形中，能够铺满地面的是（　　）

  A．正五边形

  B．正六边形

  C．正八边形

  D．正十二边形
  组卷：207引用：8难度：0.7

  解析

• 4．若x＜y,则下列不等式一定成立的是（　　）

  A．-2x＜-2y

  B．x-2＜y-2

  C．mx＞my

  D． x 2 ＞ y 2
  组卷：1138引用：19难度：0.8

  解析

• 5．下列变形正确的是（　　）

  A．由4x-5=3x+2得4x-3x=-2+5

  B．由 2 3 x-1= 1 2 x+3得4x-1=3x+3

  C．由3（x-1）=2（x+3）得3x-1=2x+6

  D．由-2x=-3得x= 3 2
  组卷：17引用：2难度：0.9

  解析

• 6．在一次防疫知识竞赛中，共有20道题，规定每答对一题得10分，答错或不答都扣5分，小明得分要不小于120分，他至少要答对多少道题？若设小明答对x道题，则下列所列不等式正确的是（　　）

  A．10x-5（20-x）＞120	B．10x-5（20-x）＜120
  C．10x-5（20-x）≤120	D．10x-5（20-x）≥120
  组卷：92引用：2难度：0.7

  解析

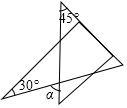• 7．将一副直角三角板按如图所示的位置放置，使含30°角的三角板的一条直角边和含45°角的三角板的一条直角边放在同一条直线上，则∠α的度数是（　　）

  A．45°

  B．60°

  C．75°

  D．85°
  组卷：7154引用：71难度：0.9

  解析

• 8．当三角形中一个内角β是另外一个内角α的

  1

  2

  时，我们称此三角形为“友好三角形”．如果一个“友好三角形”中有一个内角为54°，那么这个“友好三角形”的“友好角α”的度数为（　　）

  A．108°或27°	B．108°或54°
  C．27°或54°或108°	D．54°或84°或108°
  组卷：1130引用：9难度：0.5

  解析

三、解答题（78分）

• 24．【结论探究】如图1，在△ABC中，∠ABC的平分线BP与外角∠ACD的平分线CP相交于点P，则有结论：∠P=

  1

  2

  ∠A．
  请完成上述结论的证明过程：
  ∵BP平分∠ABC，
  ∴∠PBC=

  1

  2

  ∠

  ．
  ∵CP平分∠ACD，
  ∴∠PCD=

  1

  2

  ∠ACD．
  ∵∠ACD=∠

  +∠ABC，
  ∴∠A=∠ACD-∠ABC，
  ∵∠PCD=∠P+∠PBC，
  ∴∠P=∠PCD-∠PBC=

  1

  2

  ∠ACD-

  1

  2

  ∠

  =

  1

  2

  ∠A．
  请直接应用上面的结论解决下面问题：
  【结论应用】如图2，在△ABC中，∠A=70°，∠ABC的平分线BE与外角∠ACD的平分线CE相交于点E，外角∠HBC的平分线BF与EC的延长线相交于点F，求∠F的度数．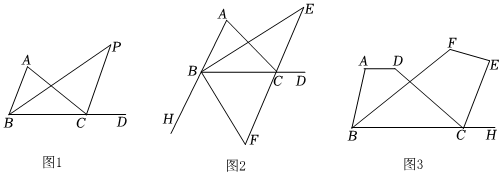
  
  【拓展应用】
  如图3，已知四边形ABCD与四边形BCEF，BF平分角∠ABC，CE平分外角∠DCH．
  ①若∠A=100°，∠D=142°，则∠E+∠F=

  °；
  ②若∠A+∠D=α，∠E+∠F=β，则α=

  （用含β的代数式表示）．
  组卷：314引用：2难度：0.5

  解析

• 25．如图，点C在线段AB上，AC=6cm,CB=4cm.点M以1cm/s的速度从点A沿线段AC向点C运动；同时点N以2cm/s的速度从点C出发，在线段CB上做往返运动（即沿C→B→C→B→…运动），当点M运动到点C时，点M、N都停止运动．设点M运动的时间为t（s）．
  
  （1）当t=1时，求MN的长．
  （2）当点C为线段MN的中点时，求t的值．
  （3）若点P是线段CN的中点，在整个运动过程中，是否存在某个时间段，使PM的长度保持不变？如果存在，求出PM的长度并写出其对应的时间段；如果不存在，请说明理由．
  组卷：176引用：4难度：0.4

  解析