2022-2023学年广东省深圳外国语学校七年级（下）期末数学试卷

一.选择题（每小题3分，共30分）

• 1．下列交通标志图案是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：1626引用：182难度：0.9

  解析

• 2．在下列以线段a,b,c的长为三边的三角形中，不能构成直角三角形的是（　　）

  A．a=1.5，b=2，c=3	B．a=5，b=12，c=13
  C．a=3，b=4，c=5	D．a=7，b=24，c=25
  组卷：195引用：1难度：0.7

  解析

• 3．下列运算正确的是（　　）

  A． 2 + 3 = 5	B． 9 1 4 = 3 1 2
  C． （ 2 - 1 ） 2022 （ 2 + 1 ） 2022 = 1	D． 3 2 - 2 = 3
  组卷：622引用：5难度：0.7

  解析

• 4．估计

  5

  ×（

  6

  -

  1

  5

  ）的值应在（　　）

  A．4和5之间

  B．5和6之间

  C．6和7之间

  D．7和8之间
  组卷：873引用：13难度：0.7

  解析

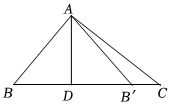• 5．如图，在Rt△ABC中，∠BAC=90°，∠C=40°，点D为BC上一点，把△ABD沿AD折叠到△AB'D，点B的对应点恰好落在边BC上，则∠CAB'的度数为（　　）

  A．10°

  B．20°

  C．30°

  D．40°
  组卷：412引用：4难度：0.8

  解析

• 6．下列说法正确的是（　　）

  A．如果一件事不是不可能发生的，那么它就必然发生

  B．“任意画一个三角形．其内角和为360°”是随机事件

  C．抛掷一枚均匀的硬币，前2次都正面朝上，第3次正面朝上的概率是0.5

  D．已知某篮球运动员投篮投中的概率为0.8，则他投10次可投中8次
  组卷：287引用：4难度：0.6

  解析

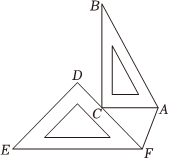• 7．如图，小明用一副三角板拼成一幅“帆船图”，∠E=45°，∠B=30°，AC∥EF，CA=CF，连结AF，则∠BAF的度数是（　　）

  A．127.5°

  B．135°

  C．120°

  D．105°
  组卷：1270引用：10难度：0.8

  解析

三.解答题（共7题，共55分）

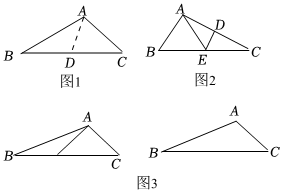• 21．如果一个三角形被一条线段分割成两个等腰三角形，那么这种分割叫做等腰分割，这条线段称为这个三角形的等腰分割线．如图1，当△ABD和△ACD为等腰三角形时，AD为△ABC的等腰分割线．
  （1）如图2，△ABC中，∠B=2∠C，线段AC的垂直平分线ED交AC于点D，交BC于点E．求证：AE是△ABC的一条等腰分割线．
  （2）如图3，在△ABC中，∠A=120°，∠B=20°，∠C=40°，请你用两种不同的方法完成△ABC的等腰分割，并直接写出每种分割之后两个等腰三角形的顶角度数．
  （3）在△ABC中，AD为△ABC的等腰分割线，且AD=BD，∠C=30°，请直接写出∠B的度数．
  ​
  组卷：453引用：3难度：0.2

  解析

• 22．已知△ABC是等腰直角三角形，∠BAC=90°，AB=AC，点D是边BC上的一个动点（不与点B，C重合），点E在直线BC上，连接AD，AE，且∠DAE=45°．
  （1）若点E是线段BC上一点，如图1，作点D关于直线AE的对称点F，连接AF，CF，EF．则BD与CF的数量关系为

  ；位置关系为

  ；
  （2）若点E是线段CB延长线上一点，如图2，作点D关于直线AE的对称点F，连接AF，BF，EF．求证：BE²+CD²=DE²；
  （3）如图3，若

  BD

  =

  8

  5

  ，

  AB

  =

  2

  ，求CE的长．
  ​​​
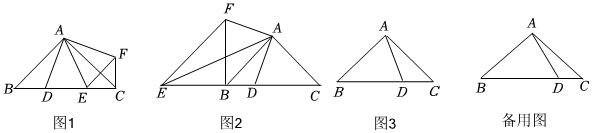  组卷：699引用：1难度：0.1

  解析