当前位置：试卷中心 > 试卷详情

2023-2024学年辽宁省丹东市凤城一中高二（上）月考数学试卷（9月份）

发布：2024/8/21 7:0:1

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1．若直线过点（1，2），（4，2+
3
），则此直线的倾斜角是（　　）
A．30° B．45° C．60° D．90°
组卷：584引用：25难度：0.9
解析
2．已知圆锥的母线长为2，侧面展开图扇形的面积为2π，那么该圆锥的体积是（　　）
A．
π
3
B．
2
π
3
C．π D．
3
π
3
组卷：399引用：9难度：0.7
解析
3．已知空间两不同直线m,n,两不同平面α、β，下列命题正确的是（　　）
A．若m∥α且n∥α，则m∥n B．若m⊥β且m⊥n,则n∥β
C．若m⊥α且m∥β，则α⊥β D．若α⊥β且m⊥α，m⊥n则n⊥β
组卷：57引用：2难度：0.9
解析
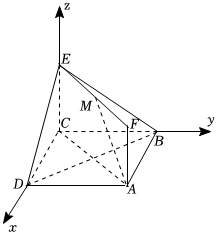4．如图，正方形ABCD与矩形ACEF所在平面互相垂直，AB=
2
，AF=1，M在EF上，且AM∥平面BDE，则M点的坐标为（　　）
A．（1，1，1） B．（
2
3
，
2
3
，1） C．（
2
2
，
2
2
，1） D．（
2
4
，
2
4
，1）
组卷：870引用：21难度：0.9
解析
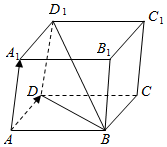5．如图，在平行六面体ABCD-A₁B₁C₁D₁中，
AB
-
AD
-
A
A
1
=（　　）
A．
A
C
1
B．
A
1
C
C．
D
1
B
D．
D
B
1
组卷：295引用：4难度：0.8
解析
6．已知k∈R，“直线l的方程是kx-y+1+2k=0”是“点（-2，1）在直线l上”的（　　）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：25引用：2难度：0.7
解析
7．已知直线
l
：
x
m
+
y
4
-
m
=
1
，若直线l与两坐标轴的正半轴围成三角形的面积最大，则直线l的方程是（　　）
A．
x
3
+
y
=
1
B．
x
+
y
3
=
1
C．
x
2
+
y
2
=
1
D．y=-x-2
组卷：197引用：2难度：0.8
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

四、解答题：本题共6小题，计70分。解答应写出文字说明、证明过程或演算步骤。

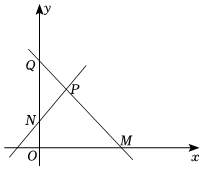21．已知直线l₁，l₂均过点P（1，2）．
（Ⅰ）若直线l₁过点A（-1，3），且l₁⊥l₂，求直线l₂的方程；
（Ⅱ）如图，O为坐标原点，若直线l₁的斜率为k,其中0＜k≤2，且与y轴交于点N，直线l₂过点
Q
（
0
，
2
R
2
+
2
）
，且与x轴交于点M，求直线l₁，l₂与两坐标轴围成的四边形PNOM面积的最小值．
组卷：89引用：4难度：0.6
解析
22．如图甲，在矩形ABCD中，AB=2AD=2
2
，E为线段DC的中点，△ADE沿直线AE折起，使得DC=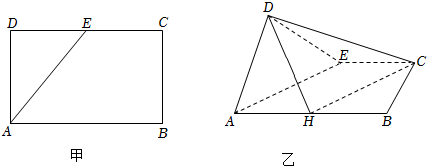
6
，如图乙．

（1）求证：BE⊥平面ADE；
（2）已知点H在线段AB上移动，设平面ADE与平面DHC所成的角为θ，求cosθ的取值范围．
组卷：155引用：6难度：0.4
解析