当前位置：试卷中心 > 试卷详情

2022-2023学年浙江省湖州市吴兴区八年级（下）期中数学试卷

发布：2024/7/5 8:0:9

一、选择题（每题3分，本大题共10小题，共30分）

1．若x为任意实数，下列各式一定是二次根式的是（　　）
A．
x
2
-
3
B．
2
（
x
+
1
）
2
C．
x
2
+
1
D．
x
2
+
2
x
组卷：803引用：2难度：0.7
解析
2．下面的图形是用数学家名字命名的，其中既是轴对称图形又是中心对称图形的是（　　）
A．
斐波那契螺旋线 B．
笛卡尔心形线
C．
赵爽弦图 D．
科克曲线
组卷：1185引用：74难度：0.8
解析
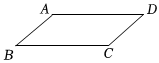3．如图，在平行四边形ABCD中，∠A：∠B=7：2，则∠A的度数是（　　）
A．110° B．140° C．120° D．160°
组卷：123引用：2难度：0.8
解析
4．下列根式中，不是最简二次根式的是（　　）
A．
5
B．
8
C．
2
2
D．
6
组卷：317引用：9难度：0.8
解析
5．有一组数据：2，5，5，6，7，这组数据的平均数为（　　）
A．3 B．4 C．5 D．6
组卷：1230引用：25难度：0.9
解析
6．用配方法解一元二次方程x²-2x-5=0，下列配方正确的是（　　）
A．（x+1）²=6 B．（x+1）²=9 C．（x-1）²=9 D．（x-1）²=6
组卷：319引用：10难度：0.9
解析
7．用反证法证明命题：“等腰三角形的底角是锐角”时，第一步可以假设（　　）
A．等腰三角形的底角是直角
B．等腰三角形的底角是直角或钝角
C．等腰三角形的底角是钝角
D．底角为锐角的三角形是等腰三角形
组卷：186引用：3难度：0.8
解析
8．若m是关于x的方程x²-2023x-1=0的根，则（m²-2023m+3）•（m²-2023m+4）的值为（　　）
A．16 B．12 C．20 D．30
组卷：512引用：2难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本大题共8小题，共66分.）

23．阅读下列材料，解答后面的问题：
在二次根式的学习中，我们不仅要关注二次根式本身的性质、运算，还要用到与分式、不等式相结合的一些运算．如：
①要使二次根式
a
-
2
有意义，则需a-2≥0，解得：a≥2；
②化简：
1
+
1
n
2
+
1
（
n
+
1
）
2
，则需计算
1
+
1
n
2
+
1
（
n
+
1
）
2
，而
1
+
1
n
2
+
1
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
（
n
+
1
）
2
+
n
2
n
2
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
n
2
+
2
n
+
1
+
n
2
n
2
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
2
n
2
+
2
n
+
1
n
2
（
n
+
1
）
2
=
n
2
（
n
+
1
）
2
+
2
n
（
n
+
1
）
+
1
n
2
（
n
+
1
）
2
=
[
n
（
n
+
1
）
+
1
]
2
n
2
（
n
+
1
）
2
所以
1
+
1
n
2
+
1
（
n
+
1
）
2
=
[
n
（
n
+
1
）
+
1
]
2
n
2
（
n
+
1
）
2
=
n
（
n
+
1
）
+
1
n
（
n
+
1
）
=
1
+
1
n
（
n
+
1
）
=
1
+
1
n
-
1
n
+
1
．
（1）根据二次根式的性质，要使
a
+
2
3
-
a
=
a
+
2
3
-
a
成立，求a的取值范围；
（2）利用①中的提示，请解答：如果
b
=
a
-
2
+
2
-
a
+
1
，求a+b的值；
（3）利用②中的结论，计算：
1
+
1
1
2
+
1
2
2
+
1
+
1
2
2
+
1
3
2
+
1
+
1
3
2
+
1
4
2
+
⋯
+
1
+
1
2022
2
+
1
2023
2
．
组卷：158引用：1难度：0.6
解析
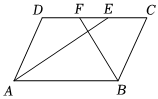24．问题：如图，在平行四边形ABCD中，AB=10，AD=6，∠DAB，∠ABC的平分线AE、BF分别与直线CD交于点E、F，请直接写出EF的长．
探究：（1）把“问题”中的条件“AB=10”去掉，其余条件不变．
①当点E与点F重合时，AB的长为
．
②当点E与点C重合时，EF的长为
．
（2）把“问题”中的条件“AB=10，AD=6”去掉，其余条件不变，当点C，D，E，F相邻两点间的距离相等时，求
AD
AB
的值．
组卷：539引用：3难度：0.5
解析