当前位置：试卷中心 > 试卷详情

2022-2023学年北京十五中高二（上）期中数学试卷

发布：2024/7/15 8:0:9

1．圆x²+y²+2y=1的半径为（　　）
A．1 B．
2
C．2 D．4
组卷：306引用：15难度：0.9
解析
2．在直角坐标系xOy中，在y轴上截距为-1且倾斜角为
3
π
4
的直线方程为（　　）
A．x+y+1=0 B．x+y-1=0 C．x-y+1=0 D．x-y-1=0
组卷：1066引用：11难度：0.9
解析
3．已知向量
a
=（-1，2，1），
b
=（3，x,y），且
a
∥
b
，那么实数x+y等于（　　）
A．3 B．-3 C．9 D．-9
组卷：148引用：23难度：0.9
解析
4．直线kx-y+1=3k,当k变动时，所有直线都通过定点（　　）
A．（0，0） B．（0，1） C．（3，1） D．（2，1）
组卷：2245引用：67难度：0.9
解析
5．“m=n”是“方程mx²+ny²=1表示圆”的（　　）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
组卷：89引用：13难度：0.9
解析
6．对于空间任意一点O，若
OP
=
1
2
OA
+
1
3
OB
+
1
6
OC
，则A，B，C，P四点（　　）
A．一定不共面 B．一定共面
C．不一定共面 D．与O点位置有关
组卷：618引用：3难度：0.8
解析
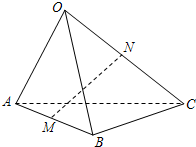7．已知三棱锥O-ABC，点M，N分别为AB，OC的中点，且
OA
=
a
，
OB
=
b
，
OC
=
c
，用
a
，
b
，
c
表示
MN
，则
MN
等于（　　）
A．
1
2
（
b
+
c
-
a
）
B．
1
2
（
a
+
b
-
c
）
C．
1
2
（
a
-
b
+
c
）
D．
1
2
（
c
-
a
-
b
）
组卷：2893引用：41难度：0.9
解析

20．如图，在三棱锥P-ABC中，底面△ABC为等边三角形，∠APC=90°，AC=2PA=4，且平面PAC⊥平面ABC．
（Ⅰ）求三棱锥P-ABC的体积；
（Ⅱ）求二面角B-AP-C的余弦值．
组卷：50引用：1难度：0.5
解析
21．已知圆C经过点A（-2，0），B（0，2），且圆心C在直线y=x上，又直线l：y=kx+1与圆C相交于P、Q两点．
（Ⅰ）求圆C的方程；
（Ⅱ）过点（0，1）作直线l₁与l垂直，且直线l₁与圆C交于M、N两点，求四边形PMQN面积的最大值．
组卷：78引用：1难度：0.5
解析

A．充分而不必要条件	B．必要而不充分条件
C．充分必要条件	D．既不充分也不必要条件

A．一定不共面	B．一定共面
C．不一定共面	D．与O点位置有关

1．圆x2+y2+2y=1的半径为（ ）