2023-2024学年江苏省常州市联盟学校高三（上）学情调研数学试卷（10月份）

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={-2，-1，1，2}，B={x|3^x＜1}，则A∩B=（　　）

  A．{-2，-1}

  B．{1，2}

  C．{-2，-1，1}

  D．{-2，-1，2}
  组卷：99引用：8难度：0.7

  解析

• 2．“x＜0”是“ln（x+1）＜0”的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充分必要条件	D．既不充分也不必要条件
  组卷：2607引用：114难度：0.9

  解析

• 3．设m,n,l是三条不同的直线，α，β，γ是三个不同的平面，有下列命题中，真命题为（　　）

  A．若m⊥n,n⊥l,则m⊥l	B．若α⊥β，β⊥γ，则α⊥γ
  C．若m⊥α，m∥n,则n⊥α	D．若m∥n,m∥α，则n∥α
  组卷：31引用：3难度：0.6

  解析

• 4．已知圆台的上下底面半径分别为1和2，侧面积为

  3

  5

  π

  ，则该圆台的体积为（　　）

  A． 8 π 3

  B． 14 π 3

  C．5π

  D． 16 π 3
  组卷：274引用：7难度：0.8

  解析

• 5．“幸福感指数”是指某个人主观地评价他对自己目前生活状态满意程度的指标，常用区间[0，10]内的一个数来表示，该数越接近10表示幸福感指数越高．已知甲、乙、丙、丁4人的幸福感指数分别为：

  4

  4

  -

  2

  3

  +

  3

  （

  -

  8

  ）

  2

  ；（（lg2）²+lg2•lg50+lg25）+log₅8×log₂25；log₂150；

  （

  5

  ）

  ln

  6

  ，则这4人的幸福感指数最高的是（　　）

  A．甲

  B．乙

  C．丙

  D．丁
  组卷：17引用：2难度：0.5

  解析

• 6．如图，该图象是下列四个函数中的某个函数的大致图象，则该函数是（　　）

  A．y= - x 3 + 3 x x 2 + 1	B．y= x 3 - x x 2 + 1
  C．y= 2 xcosx x 2 + 1	D．y= 2 sinx x 2 + 1
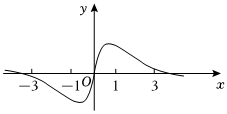  组卷：93引用：3难度：0.7

  解析

• 7．已知直线2ax-2y-a=0与曲线y=ln（2x-1）相切，则实数a为（　　）

  A． 2 e

  B． e 2 e

  C．2e

  D． e 2
  组卷：75引用：2难度：0.5

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．甲、乙两名学生进行“趣味投篮比赛”，制定比赛规则如下：每轮比赛中甲、乙两人各投一球，两人都投中或者都未投中则均记0分；一人投中而另一人未投中，则投中的记1分，未投中的记-1分，设每轮比赛中甲投中的概率为

  2

  3

  ，乙投中的概率为

  1

  2

  ，甲、乙两人投篮相互独立，且每轮比赛互不影响．
  （1）经过1轮比赛，记甲的得分为X，求X的分布列和期望；
  （2）经过3轮比赛，用P_n（n=1，2，3）表示第n轮比赛后甲累计得分低于乙累计得分的概率，研究发现点（n,P_n）（n=1，2，3）均在函数f（x）=m（s-t^x）的图象上，求实数m,s,t的值．
  组卷：25引用：4难度：0.6

  解析

• 22．已知函数f（x）=e^x+（a-1）x+cosx-2．
  （1）求曲线y=f（x）在点（0，f（0））处的切线方程；
  （2）若f（x）在（0，+∞）上单调递增，求实数a的取值范围；
  （3）当a＜0时，判断f（x）在（0，+∞）零点的个数，并说明理由．
  组卷：46引用：1难度：0.3

  解析