2022-2023学年湖北省武汉市新洲区阳逻街一中九年级（上）月考数学试卷（12月份）

一、选择题。（每小题3分，满分30分）

• 1．方程5x²=21-9x化成一般形式后，若二次项的系数为5，则它的一次项系数是（　　）

  A．9

  B．-9

  C．9x

  D．-9x
  组卷：326引用：3难度：0.8

  解析

• 2．下列电视台的台标，是中心对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：158引用：22难度：0.8

  解析

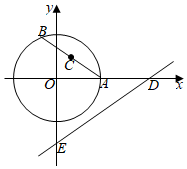• 3．如图，半径为2的⊙O与x轴的正半轴交于点A，点B是⊙O上一动点，点C为弦AB的中点，直线y=

  3

  4

  x-3与x轴、y轴分别交于点D、E，则△CDE面积的最小值为（　　）

  A．1

  B． 5

  C．3

  D．2
  组卷：1284引用：4难度：0.4

  解析

• 4．下列事件中，是必然事件的是（　　）

  A．走过一个红绿灯路口时，前方正好是红灯

  B．买一张电影票，座位号是5的倍数

  C．掷一枚质地均匀的硬币，正面向上

  D．从一个只有红球的盒子里摸出一个球是红球
  组卷：92引用：3难度：0.8

  解析

• 5．如图，在⊙€O中，

  ˆ

  AB

  =

  ˆ

  AC

  ，BC=6．AC=3

  10

  ，I是△ABC的内心，则线段OI的值为（　　）
  

  A．1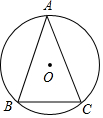

  B． 10 -3

  C．5- 10

  D． 1 3 10
  组卷：1714引用：6难度：0.3

  解析

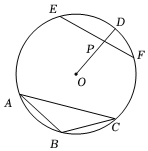• 6．如图，OD是△ABC的外接圆⊙O的半径，点P在OD上，OP=2PD，EF是经过点P的⊙O的一条弦，若∠A=30°，BC=6，则EF长的取值范围是（　　）

  A．6＜EF≤12

  B．6＜EF≤8

  C．4 5 ≤EF≤12

  D．8≤EF≤12
  组卷：131引用：2难度：0.6

  解析

• 7．在平面直角坐标系xOy中，M（x₁，y₁），N（x₂，y₂）为抛物线y=ax²+bx+c（a＞0）上任意两点，其中x₁＜x₂，设抛物线的对称轴为直线x=t,若对于x₁+x₂＞3都有y₁＜y₂，则t的取值范围为（　　）

  A．0＜t＜3

  B． t ＞ 3 2

  C． t ＜ 3 2

  D． t ≤ 3 2
  组卷：186引用：2难度：0.6

  解析

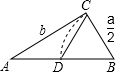• 8．欧几里得的《原本》记载，形如x²+ax=b²的方程的图解法是：画Rt△ABC，使∠ACB=90°，BC=

  a

  2

  ，AC=b,再在斜边AB上截取BD=

  a

  2

  ．则该方程的一个正根是（　　）

  A．AC的长

  B．AD的长

  C．BC的长

  D．CD的长
  组卷：7368引用：104难度：0.7

  解析

三、解答题（共八小题，满分：72分）

• 23．如图，正方形ABCD和正方形DEFG有公共顶点D．
  （1）如图1，连接AG和CE，直接写出AG和CE的关系

  ；
  （2）如图2，连接AE，M为AE中点，连接DM、CG，探究DM、CG的关系，并说明理由；
  （3）如图3，若AB=4，DE=2，直线AG与直线CE交于点P，请直接写出AP的取值范围：

  ．
  
  组卷：1817引用：4难度：0.1

  解析

• 24．如图1，抛物线y=ax²+bx+c交x轴于A、B两点，交y轴于C点．且抛物线的对称轴为直线x=2，OC=3，S_△ABC=3．
  （1）求抛物线的解析式；
  （2）如图2，过D（m,-2）作抛物线切线（不与y轴平行，且与抛物线有且仅有一个交点）DE：y=k₁x+b₁（切点为E）和DF：y=k₂x+b₂（F为切点），求k₁k₂的值；
  （3）如图3，将抛物线向左平移两个单位后再沿y轴向下运动得抛物线C₁，直线l₃及l₄为正比例函数（经过原点），直线l₃、l₄分别与（2）中直线DE、DF平行，l₃与C₁交于E，F两点，l₄与C₁交于G，H两点，M、N分别为EF、GH的中点，求点O到直线MN的距离d的最大值．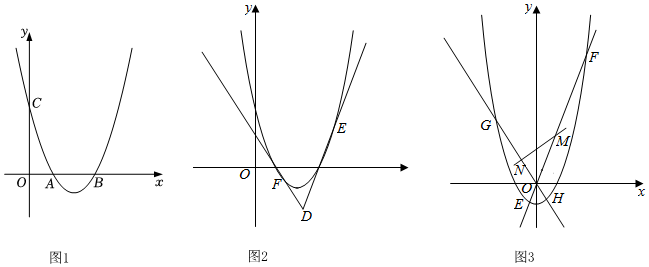
  
  组卷：616引用：4难度：0.2

  解析