2023-2024学年湖北省黄石市黄石港区教研协作体九年级（上）质检数学试卷（10月份）

一、选择题（本大题共10小题，共30.0分。在每小题列出的选项中，选出符合题目的一项）

• 1．下列y关于x的函数中，是二次函数的是（　　）

  A．y=5x2	B．y=22-2x
  C．y=2x2-3x3+1	D． y = 1 x 2
  组卷：827引用：17难度：0.7

  解析

• 2．如图是杭州2022年亚运会会徽．在选项的四个图中，能由如图经过平移得到的是（　　）

  A．

  B．

  C．

  D．
  组卷：41引用：4难度：0.7

  解析

• 3．电影《长津湖》一上映，第一天票房2.05亿元，若每天票房的平均增长率相同，三天后累计票房收入达10.53亿元，平均增长率记作x,方程可以列为（　　）

  A．2.05（1+2x）=10.53

  B．2.05（1+x）2=10.53

  C．2.05+2.05（1+x）2=10.53

  D．2.05+2.05（1+x）+2.05（1+x）2=10.53
  组卷：55引用：4难度：0.6

  解析

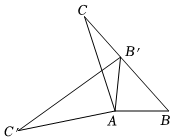• 4．如图，在△ABC中，∠BAC=108°，将△ABC绕点A按逆时针方向旋转得到△AB'C'．若点B'恰好落在BC边上，且AB'=CB'，则∠C'的度数为（　　）

  A．18°

  B．20°

  C．24°

  D．28°
  组卷：4721引用：55难度：0.7

  解析

• 5．一元二次方程x²+x-3=0的根的情况是（　　）

  A．有两个不相等的实数根	B．有两个相等的实数根
  C．只有一个实数根	D．没有实数根
  组卷：1440引用：29难度：0.9

  解析

• 6．如图，在平面直角坐标系中，将点P（2，3）绕原点O顺时针旋转90°得到点P'，则P'的坐标为（　　）

  A．（3，2）

  B．（3，-1）

  C．（2，-3）

  D．（3，-2）
  组卷：2547引用：39难度：0.8

  解析

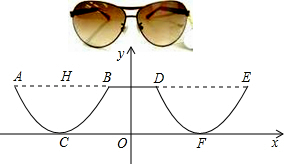• 7．为了美观，在加工太阳镜时将下半部分轮廓制作成抛物线的形状（如图所示），对应的两条抛物线关于y轴对称，AE∥x轴，AB=4cm,最低点C在x轴上，高CH=1cm,BD=2cm,则右轮廓DFE所在抛物线的解析式为（　　）

  A．y= 1 4 （x+3）2	B．y= 1 4 （x-3）2
  C．y=- 1 4 （x+3）2	D．y=- 1 4 （x-3）2
  组卷：1353引用：14难度：0.9

  解析

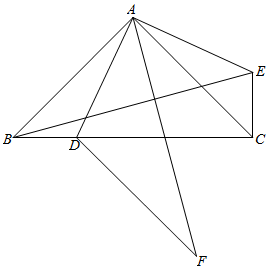• 8．如图，在Rt△ABC中，∠BAC=90°，AB=AC，D为BC边上一点，将△ABD绕点A逆时针旋转90°得到△ACE，点B、D的对应点分别为点C、E，连接BE，将AC平移得到DF（点A、C的对应点分别为点D、F），连接AF，若AB=3

  2

  ，BD=2，则AF的长为（　　）

  A． 2 10

  B．6

  C． 6 2

  D． 22
  组卷：110引用：5难度：0.6

  解析

三、解答题（本大题共8小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）

• 23．如图，在Rt△ABC中，∠ACB=90°，AC=BC，点D为AB边上一点，连结CD，过点B作BE⊥CD交CD的延长线于点E．
  
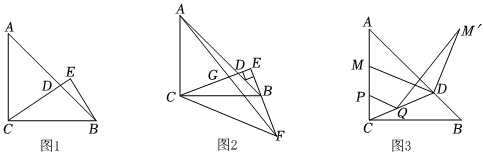
  （1）如图1，若∠BCE=2∠DBE，BE=4，求△ABC的面积；
  （2）如图2，延长EB到点F使EF=CE，分别连结CF，AF，AF交EC于点G．求证：BF=2EG；
  （3）如图3，若AC=AD，点M是直线AC上的一个动点，连结MD，将线段MD绕点D顺时针方向旋转90°得到线段M'D，点P是AC边上一点，AP=3PC，Q是线段CD上的一个动点，连结PQ，QM'．当PQ+QM'的值最小时，请直接写出∠PQM'的度数．
  组卷：617引用：3难度：0.3

  解析

• 24．如图，在平面直角坐标系中，抛物线y=ax²+bx-3（a＞0）与x轴交于A（-1，0）、B（3，0）两点，与y轴交于点C．
  （1）求抛物线的解析式；
  （2）点P为直线BC下方抛物线上的一动点，PM⊥BC于点M，PN∥y轴交BC于点N．求线段PM的最大值和此时点P的坐标；
  （3）点E为x轴上一动点，点Q为抛物线上一动点，是否存在以CQ为斜边的等腰直角三角形CEQ？若存在，请直接写出点E的坐标；若不存在，请说明理由．
  
  组卷：3825引用：12难度：0.1

  解析