当前位置：试卷中心 > 试卷详情

2023年广东省深圳市“桃李综合能力杯”数学竞赛试卷（六年级）

发布：2024/8/3 8:0:9

1．计算：16×21
1
2
-
1
1
2
×16=
。
组卷：22引用：1难度：0.8
解析
2．在2名男生和4名女生中挑选出一男一女两名主持人，有
种组合。
组卷：12引用：1难度：0.8
解析
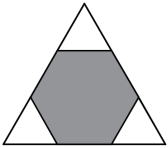3．如图所示，在一个等边三角形三边上各取三等分点，连接而成的阴影六边形为正六边形。若该正六边形的面积为120，这个等边三角形的面积为
。
组卷：22引用：1难度：0.8
解析
4．使方程两边左右相等的未知数的值叫做方程的解，例如：关于x的方程2x+7=17的解为x=5。若x=2是关于x的方程ax+6=2ax的解，则a=
。
组卷：19引用：1难度：0.5
解析
5．一个班不足50人，其中男生人数是女生人数的
6
7
，这个班最多有
人。
组卷：10引用：1难度：0.5
解析
6．小桃和小李各买了一个糖果盲盒，打开之后发现两个盲盒里面有总数相等的奶糖和水果糖两种糖，小桃的盲盒中奶糖和水果糖数量之比是2：3，小李的盲盒中奶糖和水果糖数量之比是1：2，两个盲盒中的奶糖总数与水果糖总数之比是
。
组卷：21引用：1难度：0.8
解析

17．回答下列问题，并说明理由：
（1）将一个200×199的长方形划分为若干个边长为整数的正方形，则边长为奇数的正方形至少有多少个？
（2）将一个2022×2023的长方形划分为若干个边长为整数的正方形，则边长为奇数的正方形至少有多少个？
组卷：6引用：1难度：0.5
解析
18．一个图由若干个点和若干条连接这些点的线组成。如果从图中某点出发共有n条连接线就称n为该点的桃李值，例如，在如图中，点A出发有3条连接线，则点A的桃李值为3；点B出发有2条线，则点B的桃李值就为2；……

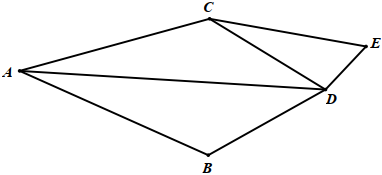
（1）如果一个图所有点的桃李值之和为2024，求这个图连接线的数量；
（2）证明：对任意的图，桃李值为奇数的点必为偶数个；
（3）一个图，若它的每个点的桃李值均不超过3，且图中任意两个点或者有直接的连接线，或者总存在另外一个点与这两个点都有连接线。请问这个图中至多有多少个点？当点数最多时，请画出一个这样的图。
组卷：4引用：1难度：0.5
解析

1．计算：16×2112-112×16=。