当前位置：试卷中心 > 试卷详情

2023-2024学年北京市人大附中九年级（上）限时训练数学试卷（10月份）

发布：2024/9/9 7:0:8

一、选择题（共24分，每题3分）

1．一元二次方程3x²-6x-4=0的二次项系数、一次项系数、常数项分别是（　　）
A．3，6，4 B．3，-6，4 C．3，6，-4 D．3，-6，-4
组卷：287引用：12难度：0.9
解析
2．将抛物线y=-x²+1向上平移2个单位，得到的抛物线表达式为（　　）
A．y=-（x+2）² B．y=-（x-2）² C．y=-x²-1 D．y=-x²+3
组卷：203引用：6难度：0.7
解析
3．下列四幅图案中，可以由如图的一笔画“天鹅”旋转180°得到的图案是（　　）
A． B． C． D．
组卷：160引用：4难度：0.8
解析
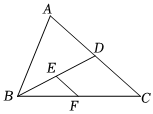4．如图，BD是△ABC的中线，E，F分别是BD，BC的中点，连接EF．若AD=4，则EF的长为（　　）
A．
3
2
B．2 C．
5
2
D．4
组卷：796引用：6难度：0.6
解析
5．用配方法解一元二次方程x²-4x+1=0，变形后的结果正确的是（　　）
A．（x+2）²=3 B．（x-2）²=3 C．（x+2）²=5 D．（x-2）²=5
组卷：659引用：9难度：0.7
解析
6．二次函数y=ax²+bx+c的x与y的部分对应值如下表：

x -1 0 1 2 3 4

y m 2 1 2 5 10

则m的值为（　　）
A．1 B．2 C．5 D．10
组卷：511引用：8难度：0.6
解析
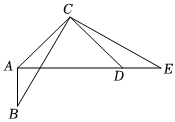7．如图，在△ABC中，∠BAC=135°，将△ABC绕点C逆时针旋转得到△DEC，点A，B的对应点分别为D，E，连接AD．当点A，D，E在同一条直线上时，下列结论不正确的是（　　）
A．△ABC≌△DEC B．∠ADC=45° C．AD=
2
AC D．AE=AB+CD
组卷：1314引用：17难度：0.6
解析
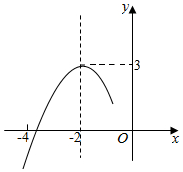8．抛物线y=ax²+bx+c的对称轴直线x=-2．抛物线与x轴的一个交点在点（-4，0）和点（-3，0）之间，其部分图象如图所示，下列结论中正确的个数有（　　）
①4a-b=0；②c≤3a；③关于x的方程ax²+bx+c=2有两个不相等实数根；④b²+2b＞4ac.
A．1个 B．2个 C．3个 D．4个
组卷：1817引用：14难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题（本题共64分，第15题8分，16-18题每题5分，19-21每题6分，第22题4分，第23、24每题6分,25题7分)

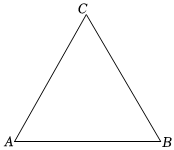24．在等边△ABC中，将线段CA绕点C逆时针旋转α（0°＜α＜30°）得到线段CD，线段CD与线段AB交于点E，射线AD与射线CB交于点F．
（1）①依题意补全图形；
②分别求∠CEB和∠AFC的大小（用含α的式子表示）；
（2）用等式表示线段BE，CE，CF之间的数量关系，并证明．
组卷：546引用：4难度：0.2
解析
25．在平面直角坐标系xOy中，已知点A（a,b）．对于点P（x,y）给出如下定义：当x≠a时，若实数k满足|y-b|=k|x-a|，则称k为点P关于点A的距离系数．若图形M上所有点关于点A的距离系数存在最小值，则称此最小值为图形M关于点A的距离系数．
（1）当点A与点O重合时，在P₁（2，2），P₂（-2，1），P₃（-4，4）中，关于点A的距离系数为1的是
；
（2）已知点B（-2，1），C（1，1），若线段BC关于点A（m,-1）的距离系数小于
1
2
，则m的取值范围为
；
（3）已知点A（4，0），T（0，t），其中2≤t≤4．以点T为对角线的交点作边长为2的正方形，正方形的各边均与某条坐标轴垂直．点D，E为该正方形上的动点，线段D，E的长度是一个定值（0＜DE＜2）．
①线段DE关于点A的距离系数的最小值为
；
②若线段DE关于点A的距离系数的最大值是
3
2
，则DE的长为
．
组卷：285引用：5难度：0.1
解析