2022-2023学年广东省中山市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的。

• 1．在锐角三角形ABC中，a=2bsinA，则B=（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 7 π 12
  组卷：334引用：7难度：0.7

  解析

• 2．已知复数z满足z²=2i,则|z|=（　　）

  A．1

  B． 2

  C．2

  D． 2 2
  组卷：126引用：6难度：0.7

  解析

• 3．已知

  |

  a

  |

  =

  3

  ，

  |

  b

  |

  =

  5

  ，设

  a

  ，

  b

  的夹角为135°，则

  b

  在

  a

  上的投影向量是（　　）

  A． - 5 2 6 a

  B． 5 2 6 a

  C． - 3 2 10 a

  D． 3 2 10 a
  组卷：296引用：6难度：0.7

  解析

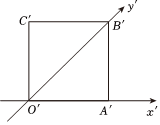• 4．一个平面图形用斜二测画法画出的直观图如图所示，此直观图恰好是一个边长为2的正方形，则原平面图形的周长为（　　）

  A．8

  B． 4 + 4 3

  C．16

  D． 8 + 8 3
  组卷：99引用：5难度：0.7

  解析

• 5．已知m,n是空间中两条不同的直线，α，β是两个不同的平面，则下列命题正确的是（　　）

  A．若m⊂α，n⊂α，m∥β，n∥β，则α∥β

  B．若α⊥β，n∥α，则n⊥β

  C．若α∥β，m∥α，则m∥β

  D．若m⊥α，n⊂β，m∥n,则α⊥β
  组卷：277引用：4难度：0.6

  解析

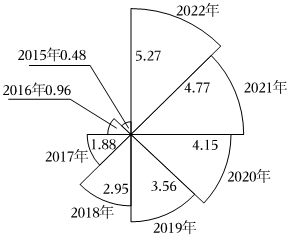• 6．南丁格尔玫瑰图是由近代护理学和护士教育创始人南丁格尔（FlorenceNightingale1820-1910）设计的，图中每个扇形圆心角都相等，半径长短表示数量大小．某机构统计了近些年中国知识付费用户数量（单位：亿人次），并绘制成南丁格尔玫瑰图如下，根据此图，下列说法错误的是（　　）

  A．2015年至2022年，知识付费用户数量逐年增加

  B．2017年至2018年，知识付费用户数量增加量为近些年来最多

  C．2022年知识付费用户数量超过2015年知识付费用户数量的10倍

  D．2016年至2022年，知识付费用户数量的年增加量逐年递增
  组卷：36引用：2难度：0.8

  解析

• 7．把函数y=cosx-

  3

  sinx的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y轴对称，则m的最小值是（　　）

  A． π 6

  B． π 3

  C． 2 π 3

  D． 5 π 6
  组卷：104引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分。解答应写出文字说明、证明过程或演算步骤。

• 21．已知△ABC满足2sinCsin（B-A）=2sinAsinC-sin²B．
  （1）试问：角B是否可能为直角？请说明理由；
  （2）若△ABC为锐角三角形，求

  sin

  C

  sin

  A

  的取值范围．
  组卷：465引用：5难度：0.6

  解析

• 22．如图1，在平行四边形ABCD中，AB=2，AD=3，∠BAD=60°，E是边BC上的点，且BE=2EC．连结AE，并以AE为折痕将△ABE折起，使点B到达点P的位置，得到四棱锥P-AECD，如图2．
  
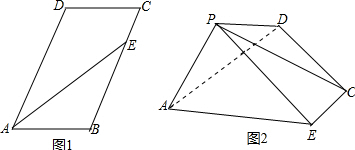
  （1）设平面PEC与平面PAD的交线为l,证明：AD∥l；
  （2）在图2中，已知PD=2．
  ①证明：平面PAE⊥平面AECD；
  ②求以P，A，D，E为顶点的四面体外接球的表面积．
  组卷：187引用：2难度：0.5

  解析