2022-2023学年湖北省武汉市江岸区、东西湖区八年级(上)期中数学试卷
发布:2024/7/25 8:0:9
一、选择题(本大题共10小题,每小题3分,共30分)下列各题中均有四个备遮容案,其中有且只有一个是正确的,济在答超卡上将正确答案的农号涂
-
1.冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一届.第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是四届冬奥会图标中的一部分,其中是轴对称图形的为( )
组卷:486引用:32难度:0.9 -
2.现有2cm,5cm长的两根木棒,再从下列长度的四根木棒中选取一根,可以围成一个三角形的是( )
组卷:741引用:14难度:0.7 -
3.已知图中的两个三角形全等,则∠α等于( )
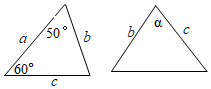 组卷:1394引用:24难度:0.8
组卷:1394引用:24难度:0.8 -
4.已知一个正多边形的一个外角为36°,则这个正多边形的边数是( )
组卷:2776引用:26难度:0.9 -
 5.如图,已知MB=ND,∠MBA=∠NDC,添加下列条件仍不能判定△ABM≌△CDN的是( )组卷:239引用:5难度:0.5
5.如图,已知MB=ND,∠MBA=∠NDC,添加下列条件仍不能判定△ABM≌△CDN的是( )组卷:239引用:5难度:0.5 -
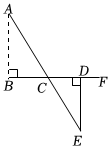 6.如图,要测量池塘两岸相对的两点A、B的距离,可以在池塘外取AB的垂线BF上的两点C、D,使得BC=CD,再画出BF的垂线DE,使点E与点A、C在一条直线上,这是测得线段DE的长就是线段AB的长,其原理运用到三角形全等的判定是( )组卷:508引用:5难度:0.7
6.如图,要测量池塘两岸相对的两点A、B的距离,可以在池塘外取AB的垂线BF上的两点C、D,使得BC=CD,再画出BF的垂线DE,使点E与点A、C在一条直线上,这是测得线段DE的长就是线段AB的长,其原理运用到三角形全等的判定是( )组卷:508引用:5难度:0.7 -
 7.如图,△ABC的外角∠ACE和外角∠CAF的平分线交于点P,已知∠P=70°,则∠B的度数为( )组卷:535引用:4难度:0.7
7.如图,△ABC的外角∠ACE和外角∠CAF的平分线交于点P,已知∠P=70°,则∠B的度数为( )组卷:535引用:4难度:0.7 -
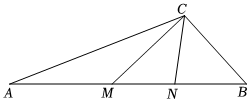 8.如图,在△ABC中,线段AC的垂直平分线和线段BC的垂直平分线分别与边AB交于点M、N(M在N的左边),设∠ACB=θ,则∠MCN的大小可以用含θ的式子表示为( )组卷:286引用:4难度:0.6
8.如图,在△ABC中,线段AC的垂直平分线和线段BC的垂直平分线分别与边AB交于点M、N(M在N的左边),设∠ACB=θ,则∠MCN的大小可以用含θ的式子表示为( )组卷:286引用:4难度:0.6
三、解答题(共8小题,共72分)下列各题需要在答题卡指定的位置写出文宇说明、证明过程、演算步骤或画出图形.
-
23.(1)问题背景:如图1,在△ABC和△ADE中,∠DAE=∠BAC,AD=AE,AB=AC,连接BD、CE,直接写出线段BD和线段CE的数量关系 ;

(2)问题探究:如图2,在△ABC和△ADE中,∠DAE=∠BAC,AD=AE,AB=AC,点E在△ABC内,延长DE交BC于点F,当点F是线段BC中点时,求证:∠ADB=90°;
(3)延伸拓展:如图3,在△ABC和△ADE中,∠DAE=∠BAC=90°,AD=AE,AB=AC,连接BE、CD,过点A作AM⊥CD于点M,反向延长AM交BE于点N,求证;CD=2AN.组卷:807引用:4难度:0.3 -
24.如图,在平面直角坐标系中,点A的坐标为(-4,0),点B的坐标为(4,0),点C的坐标为(0,4),△EDC是以点D为直角顶点的等腰直角三角形,点E在第三象限,点D在x轴上运动.

(1)如图1所示,当点D的坐标为(1,0)时,求点E的坐标;
(2)如图2所示,点D在线段OB上运动时,连接AC、BC,连接AE并延长与y轴交于点P,求点P的坐标;
(3)如图3,设△EDC的边ED与y轴交于点G,CE与x轴交于点F,当点D在线段OB上运动,且满足时,在线段DE上取点H,且DH=EG,连接HF交y轴于点Q.下列结论:①CG=2FH;②△QGH为等腰三角形,其中只有一个结论是正确,请判断出正确的结论,并写出证明过程.EG<12ED组卷:550引用:5难度:0.2


