2022-2023学年中学生标准学术能力高三（上）诊断数学试卷（12月份）

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．设复数

  z

  =

  5

  2

  -

  i

  （其中i为虚数单位），则|z|=（　　）

  A． 5

  B． 3

  C． 5 5 3

  D． 5 3 3
  组卷：25引用：2难度：0.8

  解析

• 2．已知函数y=f（x）的图象如图1所示，则图2对应的函数有可能是（　　）
  

  A．x2f（x）

  B． f （ x ） x 2

  C．xf（x）

  D．xf2（x）
  组卷：26引用：5难度：0.8

  解析

• 3．已知a,b∈（0，+∞），则“a＜b”是“log₂

  b

  3

  a

  ＞

  1

  b

  -

  1

  3

  a

  ”成立的（　　）

  A．充分不必要条件	B．必要不充分条件
  C．充要条件	D．既不充分也不必要条件
  组卷：20引用：2难度：0.5

  解析

• 4．已知一个离心率为

  1

  2

  ，长轴长为4的椭圆，其两个焦点为F₁，F₂，在椭圆上存在一个点P，使得∠F₁PF₂=60°，设△F₁PF₂的内切圆半径为r,则r的值为（　　）

  A． 3 6

  B． 2 3

  C． 2 2

  D． 3 3
  组卷：373引用：4难度：0.5

  解析

• 5．若

  tanα

  =

  （

  1

  -

  3

  tan

  20

  °

  ）

  •

  sin

  80

  °

  ，则下列可能是α的值的是（　　）

  A．20°

  B．40°

  C．50°

  D．70°
  组卷：9引用：2难度：0.6

  解析

• 6．已知f（x）=log₉x,g（x）=log₁₂x,h（x）=log₁₆x,若满足f（s）=g（t）=h（2s+t），则

  t

  s

  的值为（　　）

  A． 1 3

  B． 1 2

  C．2

  D．3
  组卷：9引用：2难度：0.6

  解析

• 7．平面向量

  a

  ，

  b

  满足

  |

  a

  |

  =

  3

  |

  b

  |

  ，且

  |

  a

  -

  b

  |

  =

  4

  ，则

  a

  与

  a

  -

  b

  夹角的正弦值的最大值为（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 2 3
  组卷：360引用：4难度：0.5

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

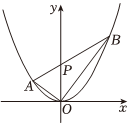• 21．如图所示，过原点O作两条互相垂直的线OA，OB分别交抛物线x²=2y于A，B两点，连接AB，交y轴于点P．
  （1）求点P的坐标；
  （2）证明：存在相异于点P的定点T，使得|PA|•|TB|=|PB|•|TA|恒成立，请求出点T的坐标，并求出△TAB面积的最小值．
  组卷：14引用：2难度：0.4

  解析

• 22．已知函数f（x）=（a-3）lnx-3ax-

  1

  x

  （

  a

  ∈

  R

  ）

  ．
  （1）试讨论f（x）的单调性；
  （2）求使得f（x）≤0在（0，+∞）上恒成立的整数a的最小值（ln3≈1.1）；
  （3）若对任意a∈（-4，-3），当x₁，x₂∈[1，4]时，均有（m+ln4）•a＞|f（x₂）-f（x₁）|+3ln4成立，求实数m的取值范围．
  组卷：222引用：4难度：0.3

  解析