2023-2024学年四川省宜宾市兴文二中高二（上）开学数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．若复数z满足

  |

  z

  •

  （

  2

  +

  i

  ）

  |

  =

  10

  ，其中i是虚数单位，则|z|²的值为（　　）

  A． 2

  B．2

  C． 3

  D．3
  组卷：14引用：3难度：0.8

  解析

• 2．已知圆柱的底面半径是3，高是4，那么圆柱的侧面积是（　　）

  A．9π

  B．12π

  C．24π

  D．36π
  组卷：110引用：4难度：0.9

  解析

• 3．若|

  a

  |=

  2

  ，|

  b

  |=2且（

  a

  -

  b

  ）⊥

  a

  ，则

  a

  与

  b

  的夹角是（　　）

  A． π 6

  B． π 4

  C． π 3

  D． 5 12 π
  组卷：753引用：53难度：0.9

  解析

• 4．某珍珠公司生产的产品中，任意抽取12颗珍珠，测得它们的直径长度（单位：mm）如下：9、8.7、8.6、8.5、8.5、8.5、8.4、8.3、8.3、8.2、8.1、8，那么在这组数据中，80%的珍珠直径长度都小于或等于（　　）

  A．8.6

  B．8.55

  C．8.25

  D．8.2
  组卷：26引用：4难度：0.7

  解析

• 5．若

  cos

  （

  θ

  -

  π

  4

  ）

  =

  2

  3

  ，则sin2θ=（　　）

  A． 2 3

  B． - 4 9

  C． - 5 9

  D． 5 9
  组卷：136引用：3难度：0.7

  解析

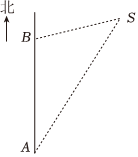• 6．如图，一艘船向正北方向航行，航行速度为每小时

  10

  39

  海里，在A处看灯塔S在船的北偏东

  θ

  （

  sinθ

  =

  3

  4

  ）

  的方向上．1小时后，船航行到B处，在B处看灯塔S在船的北偏东3θ的方向上，则船航行到B处时与灯塔S之间的距离为（　　）

  A． 10 3 海里

  B． 20 3 海里

  C． 10 13 海里

  D． 20 13 海里
  组卷：468引用：22难度：0.8

  解析

• 7．将函数f（x）=cos2x的图象向左平移φ（φ＞0）个单位长度，得到函数g（x）的图象，若函数g（x）图象关于原点对称，则φ的最小值是（　　）

  A． π 12

  B． π 6

  C． π 4

  D． π 3
  组卷：63引用：3难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

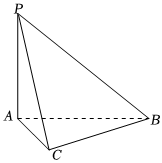• 21．如图，在三棱锥P-ABC中，∠ACB=90°，PA⊥底面ABC．
  （1）求证：平面PAC⊥平面PBC；
  （2）若AC=BC=PA，求平面PAB与平面PCB所成二面角的大小．
  组卷：111引用：5难度：0.5

  解析

• 22．已知函数f（x）=x²+x-2，g（x）=

  |

  f

  （

  x

  ）

  |

  -

  f

  （

  x

  ）

  2

  ．
  （Ⅰ）写出函数g（x）的解析式；
  （Ⅱ）若直线y=ax+1与曲线y=g（x）有三个不同的交点，求a的取值范围；
  （Ⅲ）若直线y=ax+b与曲线y=f（x）在x∈[-2，1]内有交点，求（a-1）²+（b+3）²的取值范围．
  组卷：109引用：4难度：0.3

  解析