2022-2023学年广东省深圳市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={-1，0，1，2}，B={x|0＜x＜3}，则A∩B=（　　）

  A．{-1，0，1}

  B．{0，1}

  C．{-1，1，2}

  D．{1，2}
  组卷：2575引用：43难度：0.9

  解析

• 2．设复数z满足iz=1+i（i是虚数单位），则|z|=（　　）

  A． 1 2

  B．2

  C． 2 2

  D． 2
  组卷：190引用：1难度：0.9

  解析

• 3．已知tanα=2，则cos2α=（　　）

  A． 4 5

  B． 3 5

  C． - 4 5

  D． - 3 5
  组卷：763引用：5难度：0.6

  解析

• 4．某户居民今年上半年每月的用水量（单位：t）如下：
  

  月份	1月	2月	3月	4月	5月	6月
  用水量	9.0	9.6	14.9	5.9	4.0	7.7

  小明在录入数据时，不小心把一个数据9.6录成96，则这组数据中没有发生变化的量是（　　）

  A．平均数

  B．中位数

  C．极差

  D．标准差
  组卷：190引用：2难度：0.7

  解析

• 5．已知m,n是空间两条不重合的直线，α，β是两个不重合的平面，则下列命题错误的是（　　）

  A．m∥α，m⊂β，α∩β=n,则m∥n	B．m∥n,m∥α，n⊄α，则n∥α
  C．α⊥β，m⊂α，n⊂β，则m⊥n	D．α⊥β，m⊥α，n⊥β，则m⊥n
  组卷：295引用：2难度：0.8

  解析

• 6．在梯形ABCD中，若

  AB

  =

  2

  DC

  ，且

  AC

  =

  x

  AB

  +

  y

  AD

  ，则x+y=（　　）

  A． 3 2

  B．2

  C． 5 2

  D．3
  组卷：278引用：4难度：0.7

  解析

• 7．已知正实数m,n满足m+n=2，则下列不等式恒成立的为（　　）

  A．lnm+lnn≥0

  B．m2+n2≤2

  C． 1 m + 1 n ≥2

  D． m + n ≤ 2
  组卷：391引用：1难度：0.6

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

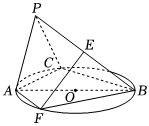• 21．如图，三棱锥P-ABC的三个顶点A，B，C在圆O上，AB为圆O的直径，且AB=6，

  PA

  =

  PC

  =

  2

  2

  ，

  BC

  =

  2

  5

  ，平面PAC⊥平面PCB，点E是PB的中点．
  （1）证明：平面PAC⊥平面ABC；
  （2）点F是圆O上的一点，且点F与点C位于直径AB的两侧．当EF∥平面PAC时，作出二面角E-BF-A的平面角，并求出它的正切值．
  组卷：504引用：1难度：0.5

  解析

• 22．已知函数

  f

  （

  x

  ）

  =

  |

  1

  4

  x

  2

  -

  x

  |

  ，g（x）=kx,f（x）与g（x）的图象恰有三个交点．
  （1）求实数k的取值范围；
  （2）用max{α，β}表示α，β中的最大值，设函数φ（x）=max{f（x），g（x）}（1⩽x⩽6），用M，m分别表示φ（x）的最大值与最小值，求M，m,并求出M-m的取值范围．
  组卷：212引用：1难度：0.4

  解析