2021-2022学年四川省成都七中高二（上）期末数学试卷（理科）（A卷）

一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={x|2a+1≤x≤3a+5}，集合B={x|3≤x≤33}，若A⊆（A∩B），则a∈（　　）

  A．[1，9]	B． [ 1 ， 28 3 ]
  C．（-∞，-4）∪[1，9]	D． （ - ∞ ，- 4 ） ∪ [ 1 ， 28 3 ]
  组卷：12引用：2难度：0.7

  解析

• 2．T=a¹⁰⁰⁰+a⁹⁹⁹（a+1）+⋯+（a+1）¹⁰⁰⁰中，a⁵²¹的系数为（　　）

  A． C 521 999

  B． C 521 1000

  C． C 521 1001

  D． C 521 1002
  组卷：4引用：2难度：0.6

  解析

• 3．复数z₁、z₂满足|z₁|=2，|z₂|=3，3z₁-2z₂=2-i,则z₁z₂的虚部为（　　）

  A． 24 5

  B． - 24 5

  C． 24 5 i

  D． - 24 5 i
  组卷：6引用：2难度：0.7

  解析

• 4．已知△ABC的三边为a、b、c.
  命题p：以a²、b²、c²为三边的三角形一定存在．
  命题q：以|a-b|+1、|b-c|+1、|c-a|+1为三边的三角形一定存在．
  则下列命题为真命题的是（　　）

  A．p∧q

  B．￢p∨q

  C．p∨￢q

  D．￢p∧￢q
  组卷：4引用：2难度：0.8

  解析

• 5．关于x的不等式（4a-3）x+b-2a≤2在[0，1]上恒成立，则a+b的最大值为（　　）

  A． 21 5

  B． 17 4

  C．4

  D． 13 3
  组卷：11引用：3难度：0.5

  解析

• 6．已知四面体ABCD中，AB⊥BC，BC⊥CD，直线AB与CD的夹角为

  π

  3

  ，BC=2，其外接球半径为

  5

  ，则其体积最大值为（　　）

  A． 4 3

  B． 6 3

  C． 4 3 3

  D． 2 3
  组卷：10引用：2难度：0.4

  解析

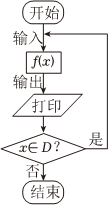• 7．对于f（x），x∈D，可构造如图所示的“数列生成机”．现给定

  f

  （

  x

  ）

  =

  4

  x

  -

  2

  x

  +

  1

  ，则下列说法正确的是（　　）

  A．若输入 x 0 = 49 65 ，则生成的数列只有四项

  B．若生成了一个无穷的常数列，则输入的x0=1

  C．若生成了一个严格递增的无穷数列，则输入的x0∈[1，2]

  D．若生成了一个严格递减的无穷数列，则输入的x0∈（2，+∞）
  组卷：22引用：2难度：0.5

  解析

[选修4-4：坐标系与参数方程]

• 22．在直角坐标系xOy中，点A（1，0），直线l：x=3．设动点M到l的距离为d,且d+|MA|=4．以点A为极点，x轴正半轴（A点右侧）为极轴，建立极坐标系．
  （1）求M轨迹Γ的极坐标方程；
  （2）直线

  m

  ：

  x = tcosα + 1

  y = tsinα

  （

  t

  为参数），与Γ交于P、Q两点，求|PQ|的最大值．
  组卷：2引用：2难度：0.5

  解析

[选修4-5：不等式选讲]

• 23．已知

  f

  （

  x

  ）

  =

  |

  1

  x

  +

  1

  |

  +

  |

  1

  -

  4

  x

  |

  ．
  （1）求f（x）的最小值m；
  （2）正实数a、b、c满足a+b+c=m,求

  S

  =

  （

  a

  +

  1

  a

  ）

  2

  +

  （

  b

  +

  1

  b

  ）

  2

  +

  （

  c

  +

  1

  c

  ）

  2

  的最小值．
  组卷：7引用：2难度：0.6

  解析