2022-2023学年山东省济宁市任城区七年级（下）期末数学试卷（五四学制）

一、选择题（本大题满分30分，每小题3分.每小题只有一个符合题意的选项，）

• 1．二元一次方程3x+2y=12的解可以是（　　）

  A． x = 0 y = 6

  B． x = 3 y = 3

  C． x = 4 y = 2

  D． x = 5 y = 0
  组卷：432引用：5难度：0.9

  解析

• 2．同时抛掷两枚质地均匀的正方体骰子1次，下列事件中是不可能事件的是（　　）

  A．朝上的点数之和为12	B．朝上的点数之和为13
  C．朝上的点数之和为2	D．朝上的点数之和小于9
  组卷：179引用：5难度：0.8

  解析

• 3．直线a∥b,其中∠1=20°，∠2=36°，∠3为（　　）

  A．56°

  B．124°

  C．34°

  D．36°
  组卷：462引用：3难度：0.6

  解析

• 4．不等式x-1≥0的解集在数轴上表示正确的是（　　）

  A．

  B．

  C．

  D．
  组卷：288引用：12难度：0.7

  解析

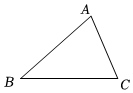• 5．如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（　　）

  A．△ABC的三条中线的交点

  B．△ABC三边的垂直平分线的交点

  C．△ABC三条角平分线的交点

  D．△ABC三条高所在直线的交点
  组卷：981引用：41难度：0.7

  解析

• 6．下列变形正确的是（　　）

  A．由a＞b,得-a＜-b	B．由a＞b,得ac＞bc
  C．由c-a＞c-b,得a＞b	D．由a＞b,得a2＞b2
  组卷：557引用：8难度：0.9

  解析

• 7．如图，直线y=kx+b（k≠0）经过点A（-2，4），则不等式kx+b＞4的解集为（　　）

  A．x＞-2

  B．x＜-2

  C．x＞4

  D．x＜4
  组卷：4064引用：31难度：0.7

  解析

• 8．如图，Rt△ABC中，∠C=90°，利用尺规在BC，BA上分别截取BE，BD，使BE=BD；分别以D，E为圆心、以大于

  1

  2

  DE的长为半径作弧，两弧在∠CBA内交于点F；作射线BF交AC于点G．若CG=1，P为AB上一动点，则GP的最小值为（　　）

  A．无法确定

  B． 1 2

  C．1

  D．2
  组卷：2450引用：38难度：0.5

  解析

三、解答题（本大题满分55分，解答要写出必要的文字说明或推演步骤

• 23．“绿水青山就是金山银山”，某村为了绿化荒山，计划在植树节当天种植柏树和杉树．经调查，购买2棵柏树和3棵杉树共需850元；购买3棵柏树和2棵杉树共需900元．
  （1）求柏树和杉树的单价各是多少元；
  （2）本次绿化荒山，需购买柏树和杉树共80棵，且柏树的棵数不少于杉树的2倍，要使此次购树费用最少，柏树和杉树各需购买多少棵？最少费用为多少元？
  组卷：1737引用：16难度：0.5

  解析

• 24．如图，平面直角坐标系中，已知点A（10，0），点B（0，8），过点B作x轴的平行线l,点P是在直线l上位于第一象限内的一个动点，连接OP，AP．
  （1）求出△AOP的面积；
  （2）已知点C是直线y=

  8

  5

  x上一点，若△APC是以AP为直角边的等腰直角三角形，求点C的坐标．
  
  组卷：133引用：1难度：0.4

  解析