当前位置：试卷中心 > 试卷详情

2022-2023学年江苏省苏州市工业园区星海中学九年级（上）月考数学试卷（12月份）

发布：2024/8/26 12:0:8

一、选择题：（本大题共有10小题，每小题3分共计30分，每小题有且只有一个答案

1．在Rt△ABC中，∠C=90°，∠B=30°，则cosB=（　　）
A．
1
2
B．
3
2
C．
3
3
D．
3
组卷：37引用：3难度：0.9
解析
2．已知一元二次方程x²-x-2=0的一个根是m,则2018-m²+m的值是（　　）
A．2015 B．2016 C．2018 D．2020
组卷：480引用：2难度：0.7
解析
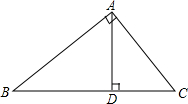3．如图，Rt△ABC中，∠A=90°，AD⊥BC于点D，若BD：CD=3：2，则tanB=（　　）
A．
3
2
B．
2
3
C．
6
2
D．
6
3
组卷：929引用：88难度：0.9
解析
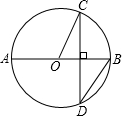4．如图，AB是⊙O的直径，AB垂直于弦CD，∠BOC=70°，则∠ABD=（　　）
A．20° B．46° C．55° D．70°
组卷：436引用：76难度：0.9
解析
5．已知y=2x²的图象是抛物线，若抛物线不动，把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是（　　）
A．y=2（x-2）²+2 B．y=2（x+2）²-2
C．y=2（x-2）²-2 D．y=2（x+2）²+2
组卷：705引用：62难度：0.9
解析
6．二次函数y=-3x²-6x+5的图象的顶点坐标是（　　）
A．（1，8） B．（-1，8） C．（-1，2） D．（1，-4）
组卷：696引用：81难度：0.9
解析
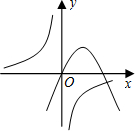7．反比例函数与二次函数在同一平面直角坐标系中的大致图象如图所示，则它们的解析式可能分别是（　　）
A．y=
k
x
，y=kx²-x B．y=
k
x
，y=kx²+x
C．y=-
k
x
，y=kx²+x D．y=-
k
x
，y=-kx²-x
组卷：423引用：39难度：0.9
解析
8．方程（a-b）x²+（b-c）x+c-a=0的一个根为x=（　　）
A．1 B．-1 C．b-c D．-a
组卷：31引用：1难度：0.7
解析
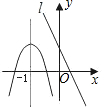9．已知抛物线和直线l在同一平面直角坐标系中的图象如图所示，抛物线的对称轴为直线x=-1，P₁（x₁，y₁）、P₂（x₂，y₂）是抛物线上的点，P₃（x₃，y₃）是直线l上的点，且-1＜x₁＜x₂，x₃＜-1，则y₁、y₂、y₃的大小关系为（　　）
A．y₁＜y₂＜y₃ B．y₃＜y₁＜y₂ C．y₃＜y₂＜y₁ D．y₂＜y₁＜y₃
组卷：704引用：43难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三、解答题：（本大题共10小题，共76分，将解答过程写在答题纸相对应的位置上.解答时应写出必要的计算过程、推演步骤或文字说明.）

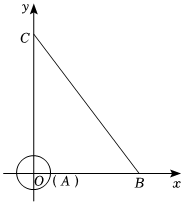27．如图，在平面直角坐标系中，半径为1的⊙A的圆心与坐标原点O重合，线段BC的端点分别在x轴与y轴上，点B的坐标为（6，0），且sin∠OCB=
3
5
．
（1）若点Q是线段BC上一点，且点Q的横坐标为m.
①求点Q的纵坐标；（用含m的代数式表示）
②若点P是⊙A上一动点，求PQ的最小值；
（2）若点A从原点O出发，以1个单位/秒的速度沿折线OBC运动，到点C运动停止，⊙A随着点A的运动而移动．
①点A从O→B的运动的过程中，若⊙A与直线BC相切，求t的值；
②在⊙A整个运动过程中，当⊙A与线段BC有两个公共点时，直接写出t满足的条件．
组卷：334引用：5难度：0.1
解析
28．如图，二次函数
y
=
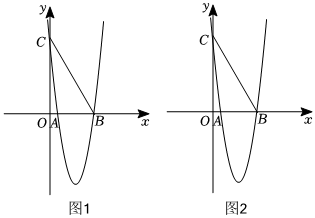3
x
2
-
6
3
x
+
5
3
的图象交x轴于A、B两点，交y轴于点C，连接BC．
（1）直接写出点B、C的坐标，B
；C
．
（2）点P是y轴右侧抛物线上的一点，连接PB、PC．若△PBC的面积
15
3
，求点P的坐标．
（3）设E为线段BC上任意一点（不含端点），连接AE，一动点M从点A出发，沿线段AE以每秒1个单位速度运动到E点，再沿线段EC以每秒2个单位的速度运动到C后停止，求点M运动时间的最小值．
（4）若点Q在y轴上，当∠AQB取得最大值时，直接写出点Q的坐标
．
组卷：102引用：1难度：0.2
解析