2023-2024学年湖南省长沙市长郡中学高三（上）月考数学试卷（三）

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={x|x²-4x+3＜0}，B={x|lnx≤1}，则A∩B=（　　）

  A．（1，e]

  B．[1，3]

  C．（0，e]

  D．（0，3]
  组卷：25引用：2难度：0.8

  解析

• 2．若i是虚数单位，则复数

  2

  +

  3

  i

  1

  +

  i

  的实部与虚部之积为（　　）

  A． - 5 4

  B． 5 4

  C． 5 4 i

  D． - 5 4 i
  组卷：667引用：6难度：0.9

  解析

• 3．函数y=2sin（

  πx

  6

  -

  π

  3

  ）（0≤x≤9）的最大值与最小值之差为（　　）

  A．2+ 3

  B．4

  C．3

  D．2- 3
  组卷：158引用：9难度：0.9

  解析

• 4．已知函数f（x）=lg（x²-4x-5）在（a,+∞）上单调递增，则a的取值范围是（　　）

  A．（2，+∞）

  B．[2，+∞）

  C．（5，+∞）

  D．[5，+∞）
  组卷：5581引用：30难度：0.6

  解析

• 5．已知F₁，F₂是双曲线C的两个焦点，P为C上一点，且∠F₁PF₂=60°，|PF₁|=3|PF₂|，则C的离心率为（　　）

  A． 7

  B． 13

  C． 7 2

  D． 13 2
  组卷：3182引用：40难度：0.7

  解析

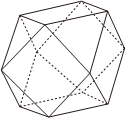• 6．“阿基米德多面体”也称为半正多面体，是由边数不全相同的正多边形为面围成的多面体，它体现了数学的对称美．如图，将一个正方体沿交于一顶点的三条棱的中点截去一个三棱锥，共可截去八个三棱锥，得到八个面为正三角形，六个面为正方形的“阿基米德多面体”，则该多面体中具有公共顶点的两个正三角形所在平面的夹角正切值为（　　）

  A． 2 2

  B．1

  C． 2

  D．2 2
  组卷：172引用：3难度：0.5

  解析

• 7．设正实数x、y、z满足4x²-3xy+y²-z=0，则

  xy

  z

  的最大值为（　　）

  A．0

  B．2

  C．1

  D．3
  组卷：477引用：4难度：0.7

  解析

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

• 21．对于椭圆：

  y

  2

  a

  2

  +

  x

  2

  b

  2

  =

  1

  （

  a

  ＞

  b

  ＞

  0

  ）

  ，我们称双曲线：

  y

  2

  a

  2

  -

  x

  2

  b

  2

  =

  1

  为其伴随双曲线．已知椭圆C：

  y

  2

  3

  +

  x

  2

  b

  2

  =

  1

  （

  0

  ＜

  b

  ＜

  3

  ），它的离心率是其伴随双曲线Γ离心率的

  2

  2

  倍．
  （1）求椭圆C伴随双曲线Γ的方程；
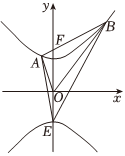
  （2）如图，点E，F分别为Γ的下顶点和上焦点，过F的直线l与Γ上支交于A，B两点，设△ABO的面积为S，∠AOB=θ（其中O为坐标原点）．若△ABE的面积为

  6

  +

  3

  3

  ，求

  S

  tanθ

  ．
  组卷：146引用：8难度：0.4

  解析

• 22．已知函数f（x）=ae^x-sinx-1，其中a∈R，e是自然对数的底数．
  （1）当a=1时，证明：对∀x∈[0，+∞），f（x）≥0；
  （2）若函数f（x）在（0，

  π

  2

  ）上存在极值，求实数a的取值范围．
  组卷：183引用：5难度：0.4

  解析