2022-2023学年山东省威海市乳山一中高二（上）月考数学试卷（12月份）

一、选择题（1-8单选题，9-12多选题）

• 1．过x+y=2与x-y=0的交点，且平行于向量

  v

  =

  （

  3

  ，

  2

  ）

  的直线方程为（　　）

  A．3x-2y-1=0

  B．3x+2y-5=0

  C．2x-3y+1=0

  D．2x-3y-1=0
  组卷：52引用：5难度：0.8

  解析

• 2．已知数列{a_n}是等比数列，满足a₅a₁₁=4a₈，数列{b_n}是等差数列，且b₈=a₈，则b₇+b₉等于（　　）

  A．24

  B．16

  C．8

  D．4
  组卷：206引用：5难度：0.7

  解析

• 3．设B是椭圆C：

  x

  2

  5

  +y²=1的上顶点，点P在C上，则|PB|的最大值为（　　）

  A． 5 2

  B． 6

  C． 5

  D．2
  组卷：6089引用：14难度：0.5

  解析

• 4．在平面直角坐标系xOy中，A（3，0），B（0，-3），点M满足

  OM

  =

  x

  OA

  +

  y

  OB

  ，x+y=1，点N为曲线y=

  -

  x

  2

  -

  2

  x

  上的动点，则|MN|的最小值为（　　）

  A． 2 2 -1

  B． 2 2

  C． 3 2 2

  D． 3 2 2 -1
  组卷：337引用：6难度：0.6

  解析

• 5．已知直三棱柱ABC-A₁B₁C₁中，∠ABC=120°，AB=2，BC=CC₁=1，则异面直线AB₁与BC₁所成角的余弦值为（　　）

  A． 3 2

  B． 15 5

  C． 10 5

  D． 3 3
  组卷：10019引用：67难度：0.6

  解析

• 6．已知数列{a_n}的前n项和S_n满足S_n=2a_n-3，则a₆=（　　）

  A．72

  B．96

  C．108

  D．126
  组卷：269引用：4难度：0.7

  解析

• 7．已知F₁，F₂分别为双曲线C：

  x

  2

  a

  2

  -

  y

  2

  b

  2

  =

  1

  （a＞0，b＞0）的左、右焦点，点A在双曲线上，且∠F₁AF₂=60°，若∠F₁AF₂的角平分线经过线段OF₂（O为坐标原点）的中点，则双曲线的离心率为（　　）

  A． 7

  B． 7 2

  C． 14

  D． 14 2
  组卷：303引用：6难度：0.6

  解析

三、解答题

• 21．已知数列{a_n}的前n项和为S_n，且a₁=-5，a₂=-2，2S_n=n（a_n-5）．
  （1）求a₃，a₄的值；
  （2）求数列{a_n}的通项公式；
  （3）若数列b_n=λ•2ⁿ-S_n为单调递增数列，求实数λ的取值范围．
  组卷：288引用：2难度：0.5

  解析

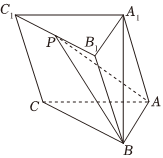• 22．如图，在三棱柱ABC-A₁B₁C₁中，AB⊥AC，AC⊥BB₁，AB=A₁B=AC=2，BB₁=2

  2

  ．
  （Ⅰ）求证：A₁B⊥平面ABC；
  （Ⅱ）若P是棱B₁C₁的中点，求直线BB₁与平面PAB所成角的正弦值．
  组卷：117引用：3难度：0.4

  解析