2022-2023学年山东省威海市环翠区新都中学九年级（上）期中数学试卷（五四学制）

一、选择题（每题3分，共36分）

• 1．在函数y=

  1

  -

  x

  x

  -

  3

  中，自变量x的取值范围是（　　）

  A．x≥0

  B．x≠3

  C．x≥0且x≠3

  D．0≤x≤3
  组卷：1347引用：3难度：0.8

  解析

• 2．如图，在平地上种植树木时，要求株距（相邻两棵树之间的水平距离）为5m,若在坡比为i=1：2.5的山坡种树，也要求株距为5m,那么相邻两棵树间的坡面距离为（　　）
  

  A．2.5m

  B．5m

  C． 29 m

  D．10m
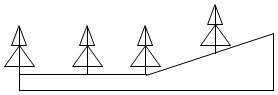  组卷：1206引用：8难度：0.5

  解析

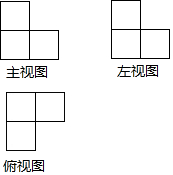• 3．一个由完全相同的小正方体组成的几何体三视图如图所示，若在这个几何体的基础上增加几个相同的小正方体，将其补成一个大正方体，则需要增加的小正方体的最少个数为（　　）

  A．4

  B．3

  C．6

  D．5
  组卷：377引用：4难度：0.7

  解析

• 4．二次函数y=ax²+|b|x+c,其对称轴为直线x=-1，若

  （

  -

  14

  3

  ，

  y

  1

  ）

  ，

  （

  5

  2

  ，

  y

  2

  ）

  ，（3，y₃）是抛物线上三点，则y₁，y₂，y₃的大小关系是（　　）

  A．y1＜y2＜y3

  B．y3＜y1＜y2

  C．y3＜y2＜y1

  D．y2＜y1＜y3
  组卷：95引用：4难度：0.5

  解析

• 5．已知抛物线y=x²-4x+3与x轴相交于点A，B（点A在点B左侧），顶点为M．平移该抛物线，使点M平移后的对应点M'落在x轴上，点B平移后的对应点B'落在y轴上，则平移后的抛物线解析式为（　　）

  A．y=x2+2x+1

  B．y=x2+2x-1

  C．y=x2-2x+1

  D．y=x2-2x-1
  组卷：4555引用：29难度：0.7

  解析

• 6．如图，在半径为

  13

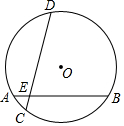  的⊙O中，弦AB与CD交于点E，∠DEB=75°，AB=6，AE=1，则CD的长是（　　）

  A．2 6

  B．2 10

  C．2 11

  D．4 3
  组卷：12135引用：31难度：0.5

  解析

• 7．已知二次函数y=x²-2px-p+3，当-1＜x＜0时，y的值恒大于1，则p的取值范围是（　　）

  A．-1≤p≤2

  B．-3≤p≤1

  C．-1≤p≤0

  D．-3≤p≤2
  组卷：268引用：4难度：0.4

  解析

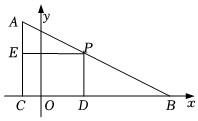• 8．如图，在△ABC中，∠ACB=90°，BC边在x轴上，A（-1，4），B（7，0）．点P是AB边上一点，过点P分别作PE⊥AC于点E，PD⊥BC于点D，当四边形CDPE的面积最大时，点P的坐标为（　　）

  A．（4， 3 2 ）

  B．（2， 5 2 ）

  C．（2，3）

  D．（3，2）
  组卷：551引用：2难度：0.3

  解析

三、解答题（共66分）

• 24．党的二十大已经胜利闭幕，各行各业的人们用拼搏奋斗凝聚起奋进新征程、建功新时代的磅礴力量，信心满怀向未来．某商店决定对某类商品进行降价促销活动：已知进价为每件6元，平时以单价12元的价格售出一天可卖80件．根据调查单价每降低1元，每天可多售出40件；设商品售价x元（售价不低于进价，x为正整数），这批商品的日利润为y元（利润=售价-成本），请解决以下问题：
  （1）当商品的售价x为多少元时，销售这批商品的日利润最大，最大值为多少？
  （2）若商店每卖一件就捐m元（m＞0）给希望小学，该店发现售价为11元时可获得最大日利润，求m的取值范围．
  组卷：62引用：2难度：0.5

  解析

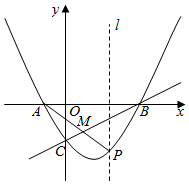• 25．已知抛物线y=ax²+bx+c与x轴交于A（-2，0）、B（6，0）两点，与y轴交于点C（0，-3）．
  （1）求抛物线的表达式；
  （2）点P在直线BC下方的抛物线上，连接AP交BC于点M，当

  PM

  AM

  最大时，求点P的坐标及

  PM

  AM

  的最大值；
  （3）在（2）的条件下，过点P作x轴的垂线l,在l上是否存在点D，使△BCD是直角三角形，若存在，请直接写出点D的坐标；若不存在，请说明理由．
  组卷：3526引用：10难度：0.3

  解析