2022-2023学年辽宁省沈阳市五校协作体高一(下)期末数学试卷
发布:2024/6/28 8:0:9
一、单选题(本大题共8小题,共40分)
-
1.已知复数z1和z2,则“z1>z2”是“z1-z2>0”的( )
组卷:203引用:3难度:0.8 -
2.已知函数
(ω>0)的图象的两个相邻对称中心之间的距离为f(x)=3tan(ωx2+π3),则ω=( )π4组卷:194引用:3难度:0.9 -
3.正四棱柱ABCD-A1B1C1D1中,AA1=3AB,则异面直线A1B与AD1所成角的余弦值为( )
组卷:589引用:11难度:0.9 -
4.已知向量
,则a=(2,1),|b|=10,|a-b|=5与a的夹角为( )b组卷:173引用:5难度:0.7 -
5.两个圆锥有等长的母线,它们的侧面展开图恰好拼成一个圆,若它们的侧面积之比为1:2,则它们的体积比是( )
组卷:500引用:10难度:0.7 -
6.两不共线的向量
,a,满足b,且∀t∈R,|a|=3|b|,则|a-tb|≥|a-b|=( )cos〈a,b〉组卷:196引用:2难度:0.5 -
7.△ABC三内角A,B,C所对边分别是a,b,c.若
,b=3,则a2+c2-3ac=b2的最大值为( )23a+c组卷:233引用:4难度:0.6
四、解答题(本大题共6小题,共70分)
-
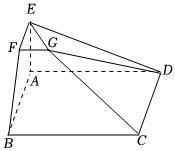 21.在如图所示的七面体ABCDEFG中,底面ABCD为正方形,EF∥AB,FG∥BC,AE⊥面ABCD.已知EF=FG=1,AB=2.
21.在如图所示的七面体ABCDEFG中,底面ABCD为正方形,EF∥AB,FG∥BC,AE⊥面ABCD.已知EF=FG=1,AB=2.
(1)设平面ABFE∩平面GCD=l,证明:l∥平面ABCD;
(2)若二面角F-BC-D的正切值为,求四棱锥D-BCGF的体积.2组卷:151引用:1难度:0.5 -
22.记△ABC的内角A,B,C的对边分别为a,b,c,已知
.1-sinAcosA=1-cos2Bsin2B
(1)求C-B的值;
(2)若△ABC的外接圆的半径为r,求的最小值.a2+b2r2sin2C组卷:118引用:1难度:0.6


