2022-2023学年甘肃省部分地市高一（下）期末数学试卷

一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

• 1．已知集合A={0，1，2}，B={1，m}．若B⊆A，则实数m的值是（　　）

  A．0

  B．2

  C．0或2

  D．0或1或2
  组卷：767引用：7难度：0.9

  解析

• 2．复数

  5

  i

  -

  2

  的共轭复数是（　　）

  A．2-i

  B．2+i

  C．-2+i

  D．-2-i
  组卷：124引用：31难度：0.9

  解析

• 3．在△ABC中，M，N，E分别是AB，AC，BC的中点，若

  AE

  =

  λ

  AM

  +

  μ

  AN

  （λ，μ∈R），则λ+μ=（　　）

  A．-2

  B．-1

  C．1

  D．2
  组卷：30引用：2难度：0.9

  解析

• 4．某校高一生物兴趣小组准备研究血型与个性的关系，小组成员经过学校同意获得了该校高一年级2000名学生的血型数据（隐藏了其它个人信息），经过数据的整理绘制如图所示的饼图，兴趣小组决定采用分层随机抽样的方法从中抽取一个容量为150的样本，则从高一年级AB型血的学生中应抽取的人数是（　　）

  A．12

  B．18

  C．24

  D．36
  组卷：38引用：1难度：0.7

  解析

• 5．已知l,m是两条不同的直线，α，β是两个不同的平面，下面正确的结论是（　　）

  A．若l∥α，m∥α，则l∥m	B．若m∥β，α⊥β，则m⊥α
  C．若l⊥α，l⊥m,则m∥α	D．若l⊥β，m⊥β，m⊥α，则l⊥α
  组卷：217引用：3难度：0.7

  解析

• 6．设a=log_0.34，b=log_0.33，c=3^0.1，d=0.3^0.2，则这四个数的大小关系是（　　）

  A．a＜b＜d＜c

  B．b＜a＜d＜c

  C．b＜a＜c＜d

  D．d＜c＜a＜b
  组卷：53引用：1难度：0.5

  解析

• 7．端午节是我国传统节日，各地端午节有吃粽子，看龙舟比赛等习俗．甲、乙、丙3人端午节准备去看龙舟比赛的概率分别是

  1

  3

  ，

  2

  5

  ，

  1

  4

  ，假定3人的行动相互之间没有影响，那么甲、乙、丙3人端午节至少有1人看龙舟比赛的概率为（　　）

  A． 7 20

  B． 2 5

  C． 2 3

  D． 7 10
  组卷：70引用：1难度：0.7

  解析

四、解答题：本题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

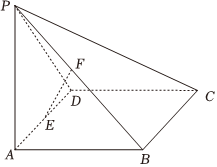• 21．如图，在四棱锥P-ABCD中，底面ABCD为边长为2的正方形，平面PAD⊥平面ABCD．PA⊥PD，PA=PD，E，F分别为AD，PB的中点．求证：
  （1）EF∥平面PCD；
  （2）平面PAB⊥平面PCD；
  （3）求四棱锥P-ABCD的体积．
  组卷：91引用：1难度：0.5

  解析

• 22．为了丰富业余生活，甲、乙、丙三人进行羽毛球比赛．比赛规则如下：①每场比赛有两人参加，并决出胜负；②每场比赛获胜的人与未参加此场比赛的人进行下一场的比赛；③依次循环，直到有一个人首先获得两场胜利，则本次比赛结束，此人为本次比赛的冠军．已知在每场比赛中，甲胜乙的概率为

  2

  3

  ，甲胜丙的概率为

  3

  5

  ，乙胜丙的概率为

  1

  2

  ．
  （1）求甲、乙、丙三人共进行了3场比赛且丙获得冠军的概率；
  （2）求甲和乙先赛且甲获得冠军的概率．
  组卷：310引用：3难度：0.6

  解析