当前位置：试卷中心 > 试卷详情

2023年广东省梅州市兴宁市中考数学二模试卷

发布：2024/7/20 8:0:8

一、选择题：本大题共10小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1．已知实数a=|-2024|，则实数a的倒数为（　　）
A．2024 B．
1
2024
C．-2024 D．
-
1
2024
组卷：335引用：8难度：0.7
解析
2．下列所述图形中，是轴对称图形但不是中心对称图形的是（　　）
A．圆 B．正方形 C．正六边形 D．正五边形
组卷：128引用：6难度：0.8
解析
3．据广东省教育考试院统计，2023年夏季高考物理类600分以上人数为27168人，历史类600分以上人数为3398人，则在本次高考中总分达600分以上人数用科学记数法表示为（　　）
A．29.556×10³ B．3.1586×10⁴ C．31.586×10³ D．3.0556×10⁴
组卷：70引用：2难度：0.5
解析
4．一元一次不等式组
3
x
+
2
≥
4
x
-
5
4
x
-
3
＜
21
的解集为（　　）
A．x＞8 B．7≤x＜8 C．x≤7 D．x＜6
组卷：256引用：3难度：0.7
解析
5．桌面上有5本书，2本为数学书，2本为物理书，1本为化学书，小明分2次从桌上抽走2本书，则小明2次抽走的都是数学书的概率为（　　）
A．
1
10
B．
1
7
C．
1
9
D．
1
12
组卷：203引用：3难度：0.5
解析
6．已知实数a=tan30°，b=sin45°，c=cos60°，则下列说法正确的是（　　）
A．b＞a＞c B．a＞b＞c C．b＞c＞a D．a＞c＞b
组卷：501引用：2难度：0.8
解析
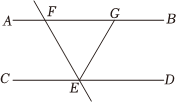7．如图所示，直线AB∥CD，直线EF交直线AB于点E，交直线CD于点F，射线EG平分∠FED，若∠AFE=130°，则∠FGE的度数为（　　）
A．55° B．65° C．75° D．85°
组卷：56引用：2难度：0.5
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

五、解答题（三）：本大题共2小题，每小题12分，共24分.

22．探究求新：已知抛物线
G
1
：
y
=
1
4
x
2
+
3
x
-
2
，将抛物线G₁平移可得到抛物线
G
2
：
y
=
1
4
x
2
．
（1）求抛物线G₁平移得到抛物线G₂的平移路径；
（2）设T（0，t），直线l：y=-t,是否存在这样的t,使得抛物线G₂上任意一点到T的距离等于到直线l的距离？若存在，求出t的值；若不存在，试说明理由；
（3）设H（0，1），Q（1，8），M为抛物线G₂上一动点，试求QM+MH的最小值．
参考公式：若点M（x₁，y₁），N（x₂，y₂）为平面上两点，则有
MN
=
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
．
组卷：76引用：2难度：0.3
解析
23．综合运用：在等腰梯形ABCD中，如图1所示，AB∥CD，AD=BC，∠DAC=90°，
AC
=
BD
=
3
，
sin
∠
ACD
=
1
2
，连接对角线AC，BD相交于点T．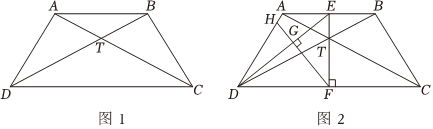

（1）求证：AB•TD=CD•BT=α，并求出实数α的值；
（2）若以T为圆心，TB为半径作圆，求该圆⊙T与直线CD的位置关系并给出证明；
（3）如图2所示，过点T作EF⊥CD，点E在AB上，点F在CD上，连接ED，过点F作FG⊥ED并延长FG交AD于点H，求△HGD的面积．
组卷：47引用：2难度：0.1
解析