2023-2024学年江苏省南京市六校联考高三（上）月考数学试卷（8月份）
发布：2024/8/7 8:0:9
一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.
-
1．若复数z满足z（1+i）=2i,则|z|等于（ ）
组卷：63引用：8难度：0.9 -
2．已知集合A={x|x2+x-2＜0}，B={x|lgx＜1}，A∩B=（ ）
组卷：88引用：6难度：0.8 -
3．等差数列{an}的前n项和为Sn，且a2=5，a4+a8=26，则S7=（ ）
组卷：171引用：2难度：0.7 -
4．从2位男生，3位女生中安排3人到三个场馆做志愿者，每个场馆各1人，且至少有1位男生入选，则不同安排方法有（ ）种
组卷：178引用：1难度：0.5 -
5．“m=8”是“直线5x+12y+m=0与圆x2+y2-2x=0相切”的（ ）条件．
组卷：40引用：2难度：0.6 -
6．在平面直角坐标系xOy中，双曲线C：
x2a2=1（a＞0，b＞0）的左、右焦点分别为F1，F2，过F2且垂直于x轴的直线与C交于P，Q两点，F1Q与y轴的交点为R，F1Q⊥PR，则C的离心率为（ ）-y2b2组卷：1072引用：9难度：0.5 -
7．已知
，则tan（π3+θ）=34=（ ）sin（2θ+π6）组卷：50引用：1难度：0.7
四、解答题：本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.
-
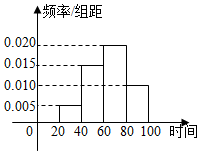21．2019年春节期间，我国高速公路继续执行“节假日高速公路免费政策”．某路桥公司为掌握春节期间车辆出行的高峰情况，在某高速公路收费站点记录了大年初三上午9：20～10：40这一时间段内通过的车辆数，统计发现这一时间段内共有600辆车通过该收费点，它们通过该收费点的时刻的频率分布直方图如图所示，其中时间段9：20～9：40记作区[20，40），9：40～10：00记作[40，60），10：00～10：20记作[60，80），10：20～10：40记作[80，100），例如10点04分，记作时刻64．
（1）估计这600辆车在9：20～10：40时间内通过该收费点的时刻的平均值（同一组中的数据用该组区间的中点值代表）；
（2）为了对数据进行分析，现采用分层抽样的方法从这600辆车中抽取10辆，再从这10辆车随机抽取4辆，设抽到的4辆车中，在9：20～10：00之间通过的车辆数为X，求X的分布列与数学期望；
（3）由大数据分析可知，车辆在每天通过该收费点的时刻T服从正态分布N（μ，σ2），其中μ可用这600辆车在9：20～10：40之间通过该收费点的时刻的平均值近似代替，σ2可用样本的方差近似代替（同一组中的数据用该组区间的中点值代表），已知大年初五全天共有1000辆车通过该收费点，估计在9：46～10：40之间通过的车辆数（结果保留到整数）．
若T～N（μ，σ2）则P（μ-σ＜T≤μ+σ）=0.6827，P（μ-2σ＜T≤μ+2σ）=0.9545，P（μ-3σ＜T≤μ+3σ）=0.9973．组卷：286引用：10难度：0.4 -
22．已知函数f（x）=ex+x2-x,g（x）=x2+ax+b,a,b∈R．
（1）当a=1时，求函数F（x）=f（x）-g（x）的单调区间；
（2）若曲线y=f（x）在点（0，1）处的切线l与曲线y=g（x）切于点（1，c），求a,b,c的值；
（3）若f（x）≥g（x）恒成立，求a+b的最大值．组卷：1241引用：13难度：0.1
