2023-2024学年浙江省金衢山五校联盟九年级（上）质检数学试卷（10月份）

一、选择题（本题有10小题，每小题3分，共30分.请选出各题中唯一的正确选项，不选、多选、错选，均不给分）

• 1．下列事件为必然事件的是（　　）

  A．口袋中装有2个红球和1个白球，从中摸出2个球，其中必有红球

  B．明天会下雪

  C．开电视机，CCTV第一套节目正在播放新闻

  D．购买一张彩票中奖一百万元
  组卷：89引用：3难度：0.8

  解析

• 2．若y=（m-2）

  x

  m

  2

  -

  2

  -x+1是二次函数，则m的值是（　　）

  A．4

  B．2

  C．-2

  D．-2或2
  组卷：1662引用：13难度：0.5

  解析

• 3．已知某二次函数上两点A（x₁，y₁），B（x₂，y₂），当1＜x₁＜x₂时，（x₂-x₁）（y₂-y₁）＞0；当x₁＜x₂＜1时，（x₂-x₁）（y₂-y₁）＜0，则该二次函数的解析式可以是（　　）

  A．y=2（x+1）2

  B．y=2（x-1）2

  C．y=-2（x+1）2

  D．y=-2（x-1）2
  组卷：347引用：3难度：0.5

  解析

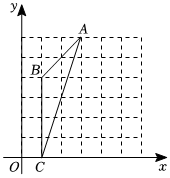• 4．如图，在平面直角坐标系xOy中，A（3，6），B（1，4），C（1，0），则△ABC外接圆的圆心坐标是（　　）

  A．（4，2）

  B．（4，3）

  C．（5，3）

  D．（5，2）
  组卷：1186引用：9难度：0.5

  解析

• 5．在同一平面直角坐标系中，函数y=mx+m和函数y=-mx²+2x+2（m是常数，且m≠0）的图象可能是（　　）

  A．

  B．

  C．

  D．
  组卷：2619引用：47难度：0.7

  解析

• 6．如图所示，这个图案可以看作是以“基本图案”——原图案的四分之一经过变换形成的，但一定不能通过变换得到（　　）

  A．旋转

  B．轴对称

  C．平移

  D．对称和旋转
  组卷：118引用：1难度：0.5

  解析

• 7．某商品现在的售价为每件60元，每星期可卖出300件．市场调查反映，如果调整商品售价，每降价1元，每星期可多卖出20件．设每件商品降价x元后，每星期售出商品的总销售额为y元，则y与x的关系式为（　　）

  A．y=60（300+20x）	B．y=（60-x）（300+20x）
  C．y=300（60-20x）	D．y=（60-x）（300-20x）
  组卷：5164引用：31难度：0.7

  解析

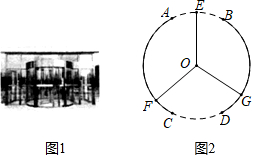• 8．如图1为某酒店的圆形旋转门，可看成如图2由外围的⊙O和3翼隔风玻璃组成，外围圆有通道弧AB和弧CD，且它们关于圆心O中心对称，圆内的3翼隔风玻璃可绕圆心O转动，且所成的夹角∠EOF=∠FOG=∠GOE=120°，3翼隔风玻璃在转动过程中，始终使大厅内外空气隔离，起到对大厅内保温作用．例如：当隔风玻璃转到如图2位置时，大厅内外空气被隔风玻璃OF，OG隔离．则通道弧AB所对圆心角的度数的最大值为（　　）

  A．30°

  B．60°

  C．90°

  D．120°
  组卷：268引用：3难度：0.6

  解析

三、解答题（本题有8小题，第17～19题每题6分，第20、21题每题8分，第22、23题每题10分，第24题12分，共66分）

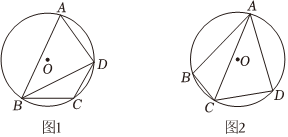• 23．定义：有一个角是其对角一半的圆的内接四边形叫做圆美四边形，其中这个角叫做美角．
  
  （1）如图1，若四边形ABCD是圆美四边形，求美角∠BAD的度数；
  （2）在（1）的条件下，若⊙O的半径为4．
  ①求BD的长；
  ②连接CA，若CA平分∠BCD，如图2，请判断BC、CD、AC之间有怎样的数量关系，并说明理由．
  组卷：152引用：4难度：0.1

  解析

• 24．已知抛物线y=a（x-m）²+

  1

  2

  m+4（am≠0）过点A（0，4）．
  （1）若m=2时，求a的值；
  （2）如图1，顶点M在第一象限，B、C是抛物线对称轴l上的两点，且MB=MC，在直线l右侧以BC为边作正方形BCDE，点E恰好在抛物线上．
  ①求am的值；
  ②试判断点E和点A是否关于直线l对称？如果对称，请说明理由，如果不对称，请举出反例．
  ③如图2，作直线CE，请说明直线CE始终在抛物线y=a（x-m）²+

  1

  2

  m+4的上方（除E点外）．
  
  组卷：319引用：3难度：0.3

  解析