定义：有一个角是其对角一半的圆的内接四边形叫做圆美四边形，其中这个角叫做美角．
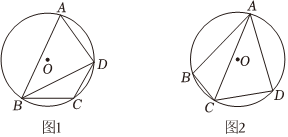
（1）如图1，若四边形ABCD是圆美四边形，求美角∠BAD的度数；
（2）在（1）的条件下，若⊙O的半径为4．
①求BD的长；
②连接CA，若CA平分∠BCD，如图2，请判断BC、CD、AC之间有怎样的数量关系，并说明理由．
【考点】圆的综合题．
【答案】（1）∠BAD=60°；
（2）①BD的长为4；
②AC=BC+CD，理由见解答过程．
（2）①BD的长为4
3
②AC=BC+CD，理由见解答过程．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/14 16:0:8组卷：153引用：4难度：0.1
相似题
-
1．已知到直线l的距离等于a的所有点的集合是与直线l平行且距离为a的两条直线l1、l2（如图①）．
（1）在图②的平面直角坐标系中，画出到直线y=x+2的距离为1的所有点的集合的图形．并写出该图形与y轴交点的坐标．2
（2）试探讨在以坐标原点O为圆心，r为半径的圆上，到直线y=x+2的距离为1的点的个数与r的关系．2
（3）如图③，若以坐标原点O为圆心，2为半径的圆上只有两个点到直线y=x+b的距离为1，则b的取值范围为 ．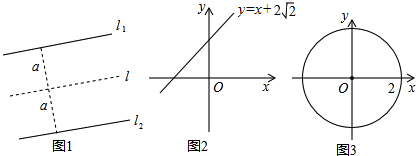
发布：2025/6/21 6:0:2组卷：516引用：9难度：0.5 -
2．如图1，直线l：y=-
x+b与x轴交于点A（4，0），与y轴交于点B，点C是线段OA上一动点（0＜AC＜34）．以点A为圆心，AC长为半径作⊙A交x轴于另一点D，交线段AB于点E，连接OE并延长交⊙A于点F．165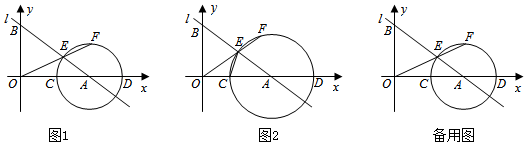
（1）求直线l的函数表达式和tan∠BAO的值；
（2）如图2，连接CE，当CE=EF时，
①求证：△OCE∽△OEA；
②求点E的坐标；
（3）当点C在线段OA上运动时，求OE•EF的最大值．发布：2025/6/20 11:30:2组卷：5310引用：10难度：0.1 -
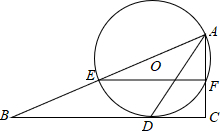3．如图，在Rt△ABC中，∠C=90°，AD平分∠BAC交BC于点D，O为AB上一点，经过点A，D的圆O分别交AB，AC于点E，F，连接EF．
（1）求证：BC是圆O的切线；
（2）求证：AD2=AF•AB；
（3）若BE=16，sinB=，求AD的长．513发布：2025/6/22 0:0:2组卷：1174引用：7难度：0.2
