2020-2021学年湖北省武汉市武昌区粮道街中学九年级（上）月考数学试卷（10月份）

一、选择题（共10小题，每小题3分，共30分）

• 1．一元二次方程2x²-3x-1=0的二次项系数和一次项系数分别是（　　）

  A．2，3

  B．2，-3

  C．2，-1

  D．-3，0
  组卷：171引用：4难度：0.9

  解析

• 2．一元二次方程x²-5x=0的根是（　　）

  A．5

  B．0

  C．0或5

  D．0或-5
  组卷：70引用：10难度：0.9

  解析

• 3．抛物线y=3（x-1）²+2的顶点坐标是（　　）

  A．（1，-2）

  B．（-1，2）

  C．（1，2）

  D．（-1，-2）
  组卷：254引用：13难度：0.9

  解析

• 4．将抛物线

  y

  =

  1

  2

  x

  2

  向左平移2个单位，再向上平移1个单位后，所得抛物线解析式为（　　）

  A． y = 1 2 （ x + 2 ） 2 + 1	B． y = 1 2 （ x - 2 ） 2 + 1
  C． y = 1 2 （ x + 2 ） 2 - 1	D． y = 1 2 （ x - 2 ） 2 - 1
  组卷：17引用：2难度：0.5

  解析

• 5．一元二次方程x²+3x-3=0的根的情况是（　　）

  A．有两个相等实数根	B．有两个不相等实数根
  C．没有实数根	D．无法确定
  组卷：9引用：1难度：0.5

  解析

• 6．设x₁、x₂是一元二次方程x²-2x-3=0的两个根，则x₁+x₂的值为（　　）

  A．-2

  B．-3

  C．2

  D．3
  组卷：1589引用：50难度：0.9

  解析

• 7．某校九年级（1）班学生毕业时，每个同学都将自己的相片向全班其他同学各送一张留作纪念，全班共送了1980张相片，如果全班有x名学生，根据题意，列出方程为（　　）

  A． x （ x - 1 ） 2 = 1980	B．x（x+1）=1980
  C．2x（x+1）=1980	D．x（x-1）=1980
  组卷：1123引用：16难度：0.7

  解析

• 8．如图，坐标平面上，二次函数y=-x²+4x-k的图象与x轴交于A，B两点，与y轴交于C点，其顶点为D，且k＞0．若△ABC与△ABD的面积比为1：4，则k的值为（　　）

  A．1

  B． 4 3

  C． 1 2

  D． 4 5
  组卷：91引用：2难度：0.6

  解析

三、解答题（共8个小题，共72分）

• 23．我们定义：如图1，在△ABC中，把AB点绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接BC．当α+β=180°时，我们称△A′B′C′是△ABC的“旋补三角形”，△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．
  特例感知：
  （1）在图2，图3中，△AB′C′是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．
  ①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD=

  BC．
  ②如图3，当∠BAC=90°，BC=8时，则AD长为

  ．
  [猜想论证]
  （2）图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．
  [拓展应用]
  （3）如图4，在四边形ABCD内部恰好存在一点P，使△PDC是△PAB的“旋补三角形”，自行补图形，
  ∠C=∠PDC=90°，BC=90°，CD=2

  3

  ，DA=6．直接写出△PAB的“旋补中线”长是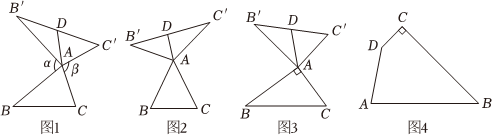

  ．
  
  组卷：85引用：1难度：0.1

  解析

• 24．如图，直线y=-

  1

  2

  x+2交y轴于点A，交x轴于点C，抛物线y=-

  1

  4

  x²+bx+c经过点A，点C，且交x轴于另一点B．
  （1）直接写出点A，点B，点C的坐标及抛物线的解析式；
  （2）在直线AC上方的抛物线上有一点M，求四边形ABCM面积的最大值及此时点M的坐标；
  （3）将线段OA绕x轴上的动点P（m,0）顺时针旋转90°得到线段O′A′，若线段O′A′与抛物线只有一个公共点，请结合函数图象，求m的取值范围．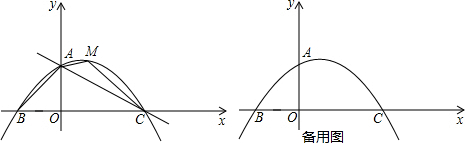
  
  组卷：3040引用：13难度：0.2

  解析