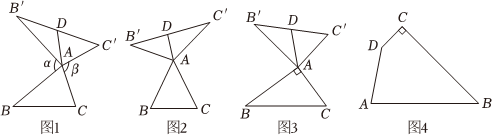
我们定义：如图1，在△ABC中，把AB点绕点A顺时针旋转α（0°＜α＜180°）得到AB'，把AC绕点A逆时针旋转β得到AC'，连接BC．当α+β=180°时，我们称△A′B′C′是△ABC的“旋补三角形”，△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．
特例感知：
（1）在图2，图3中，△AB′C′是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．
①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD=1212BC．
②如图3，当∠BAC=90°，BC=8时，则AD长为 44．
[猜想论证]
（2）图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明．
[拓展应用]
（3）如图4，在四边形ABCD内部恰好存在一点P，使△PDC是△PAB的“旋补三角形”，自行补图形，
∠C=∠PDC=90°，BC=90°，CD=23，DA=6．直接写出△PAB的“旋补中线”长是 3939．
1
2
1
2
3
39
39
【考点】四边形综合题．
【答案】；4；
1
2
39
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/28 14:0:8组卷：85引用：1难度：0.1
相似题
-
1．如图，点P是正方形ABCD对角线AC上一动点，点E在射线BC上，且PE=PB，连接PD，O为AC中点．
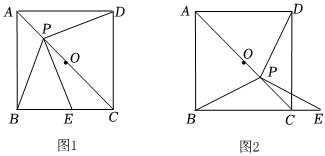
（1）如图1，当点P在线段OA上时，试猜想PE与PD的数量关系和位置关系．
（2）如图2，当点P在线段OC上时，（1）中的猜想还成立吗？请说明理由．
（3）如图2，试用等式来表示PB、BC、CE之间的数量关系：．发布：2025/6/8 18:0:1组卷：53引用：1难度：0.1 -
2．按要求回答下列问题：
发现问题．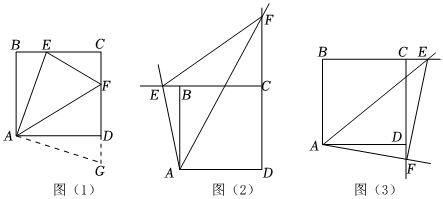
（1）如图（1），在正方形ABCD中，点E，F分别是BC，CD边上的动点，且∠EAF=45°，易证：EF=DF+BE．（不必证明）；
（2）类比延伸
①如图（2），在正方形ABCD中，如果点E，F分别是边BC，CD延长线上的动点，且∠EAF=45°，则（1）中的结论还成立吗？请写出证明过程；
②如图（3），如果点E，F分别是边BC，CD延长线上的动点，且∠EAF=45°，则EF，BE，DF之间的数量关系是 ．（不要求证明）
（3）拓展应用：如图（1），若正方形的ABCD边长为6，，求EF的长．AE=35发布：2025/6/8 18:30:1组卷：235引用：4难度：0.1 -
3．定义：四边形ABCD中，将对角线AC和BD的平方和，即AC2+BD2的值称为四边形ABCD的“特征数”．
（1）①在菱形ABCD中，AB=4，∠BAD=60°，则菱形ABCD的“特征数”=；
②正方形EFGH的“特征数”等于16，则边长=；
（2）平行四边形ABCD中，AB=a,BC=b,试证明：平行四边形ABCD的“特征数”为2a2+2b2；
（3）利用（2）的结论解决下列问题：
平行四边形ABCD中，，BC=6，且AC⋅BD=60，AC＜BD，试求AC和BD的长度．AB=42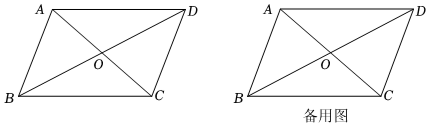
发布：2025/6/8 15:0:1组卷：373引用：3难度：0.2
