2022-2023学年天津市经开二中高三（上）期中数学试卷

一、单选题（本大题共9小题，共45分）

• 1．已知集合A={x|-2＜x＜4}，B={x|x≥2}，则A∩（∁_RB）=（　　）

  A．（2，4）

  B．（-2，4）

  C．（-2，2）

  D．（-2，2]
  组卷：200引用：12难度：0.9

  解析

• 2．命题“a＞b”是“

  1

  a

  ＜

  1

  b

  ”的（　　）

  A．既不充分又不必要条件	B．充要条件
  C．必要不充分条件	D．充分不必要条件
  组卷：165引用：2难度：0.7

  解析

• 3．函数f（x）=

  3

  x

  2

  cosx

  e

  x

  -

  e

  -

  x

  的部分图象大致为（　　）

  A．

  B．

  C．

  D．
  组卷：252引用：6难度：0.7

  解析

• 4．已知a=

  5

  1

  5

  ，b=lo

  g

  4

  5

  ，c=log₅2，则a,b,c的大小关系为（　　）

  A．a＞b＞c

  B．a＞c＞b

  C．b＞a＞c

  D．c＞b＞a
  组卷：40引用：1难度：0.9

  解析

• 5．下列各式化简运算结果为1的是（　　）

  A．log53×log32×log25	B．lg 2 + 1 2 lg5
  C． lo g a a2（a＞0且a≠1）	D．eln3- （ 0 . 125 ） - 1 3
  组卷：300引用：5难度：0.8

  解析

• 6．已知向量

  a

  =

  （

  2

  ，

  3

  ）

  ，

  b

  =

  （

  -

  1

  ，

  3

  ）

  ，则

  a

  在

  b

  上的投影向量为（　　）

  A． （ - 1 4 ， 3 4 ）

  B． （ 1 4 ，- 3 4 ）

  C． （ 1 2 ，- 3 2 ）

  D． （ - 1 2 ， 3 2 ）
  组卷：455引用：8难度：0.5

  解析

三、解答题（本大题共5小题，共75分。解答应写出文字说明，证明过程或演算步骤）

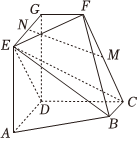• 19．如图，AD∥BC且AD=2BC，AD⊥CD，EG∥AD且EG=AD，CD∥FG且CD=2FG，DG⊥平面ABCD，DA=DC=DG=2．
  （1）若M为CF的中点，N为EG的中点，求证：MN∥平面CDE；
  （2）求二面角E-BC-F的正弦值；
  （3）若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求点P到平面CDE的距离．
  组卷：60引用：6难度：0.5

  解析

• 20．已知数列{a_n}满足a_n+1-a_n=1，其前5项和为15；数列{b_n}是等比数列，且b₁=2，4b₂，2b₃，b₄成等差数列．
  （Ⅰ）求{a_n}和{b_n}的通项公式；
  （Ⅱ）设数列{b_n}的前n项和为S_n，证明：S_n•S_n+2=

  S

  2

  n

  +

  1

  -b_n+2（n∈N^*）；
  （Ⅲ）比较

  n

  ∑

  i

  =

  1

  a

  i

  b

  n

  +

  1

  -

  i

  和

  2

  n

  -

  1

  ∑

  i

  =

  1

  （

  -

  1

  ）

  i

  -

  1

  a

  2

  i

  的大小（n∈N^*）．
  组卷：420引用：2难度：0.5

  解析