2022-2023学年河南省焦作市高一（下）期末数学试卷

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

• 1．已知集合A={x|lnx＜0}，B={x|x²-2x-3≤0}，则（∁_RA）∪B=（　　）

  A．{x|1＜x＜3}

  B．{x|0≤x≤1}

  C．∅

  D．R
  组卷：94引用：2难度：0.8

  解析

• 2．已知复数z满足（1+i）²z=2+4i,则复数z的共轭复数

  z

  =（　　）

  A．2+i

  B．2-i

  C．-2+i

  D．-2-i
  组卷：32引用：2难度：0.8

  解析

• 3．已知角α的顶点在坐标原点，始边在x轴的非负半轴上，终边经过点P（1，-2），则tan2α=（　　）

  A． - 4 3

  B． 4 3

  C． - 8 3

  D． 8 3
  组卷：85引用：2难度：0.8

  解析

• 4．设a=3^0.8，

  b

  =

  （

  1

  3

  ）

  -

  0

  .

  7

  ，

  c

  =

  1

  2

  lo

  g

  2

  3

  ，则a,b,c的大小关系为（　　）

  A．c＜b＜a

  B．c＜a＜b

  C．b＜a＜c

  D．b＜c＜a
  组卷：143引用：5难度：0.7

  解析

• 5．在△ABC中，边BC上的中线与边AC上的中线的交点为E，若

  CE

  =

  λ

  AB

  +

  μ

  AC

  ，则λ+μ=（　　）

  A．1

  B．-1

  C． 1 3

  D． - 1 3
  组卷：104引用：4难度：0.7

  解析

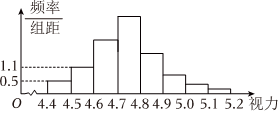• 6．随机抽查了某校100名高三学生的视力情况，得到的频率分布直方图如图所示，由于不慎将部分数据丢失，但知道后5组的频数和为64，设视力在4.6到4.8之间的学生人数为a,各组中频率最大的为0.34，则a的值为（　　）

  A．64

  B．54

  C．48

  D．27
  组卷：41引用：3难度：0.7

  解析

• 7．已知函数

  f

  （

  x

  ）

  =

  co

  s

  2

  （

  x

  -

  π

  3

  ）

  -

  co

  s

  2

  x

  ，有下述三个结论：
  ①f（x）的最小正周期是π；
  ②f（x）在区间

  （

  π

  6

  ，

  π

  2

  ）

  上不单调；
  ③将f（x）图象上的所有点向右平移

  π

  12

  个单位长度后，得到函数

  g

  （

  x

  ）

  =

  3

  2

  cos

  2

  x

  的图象．
  其中所有正确结论的编号是（　　）

  A．①

  B．②

  C．①②

  D．①②③
  组卷：70引用：2难度：0.7

  解析

四、解答题：共70分．解答应写出文字说明，证明过程或演算步骤．

• 21．已知函数

  f

  （

  x

  ）

  =

  2

  x

  -

  1

  ，g（x）=log₂（x-1）．
  （1）若λ＞0，函数h（x）=f（x）-λg（x）在区间（3，5）上存在零点，求λ的取值范围；
  （2）若a＞1，且对任意x₁∈[a,a+3]，都有x₂∈[a,a+3]，使得f（x₁）≤g（x₂）成立，求a的取值范围．
  组卷：27引用：3难度：0.5

  解析

• 22．已知在△ABC中，a,b,c分别是内角A，B，C所对的边，且

  c

  2

  b

  -

  a

  =

  cos

  C

  cos

  A

  ．
  （1）求C；
  （2）若a=1，b=3，CD为∠ACB的平分线，求CD的长；
  （3）若acosB+bcosA=2，且△ABC为锐角三角形，求△ABC面积的取值范围．
  组卷：160引用：2难度：0.5

  解析