当前位置：试卷中心 > 试卷详情

2023年江苏省扬州市邗江区世明双语学校中考数学四模试卷

发布：2024/5/23 8:0:8

一.选择题（共8小题，满分24分，每小题3分）

1．下列运算正确的是（　　）
A．
12
-
3
=
3
B．（-3）²=6 C．3a⁴-2a²=a² D．（-a³）²=a⁵
组卷：238引用：4难度：0.9
解析
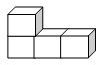2．如图，图中的几何体中，它的左视图是（　　）
A． B． C． D．
组卷：95引用：42难度：0.9
解析
3．下列二次根式中与
2
是同类二次根式的是（　　）
A．
12
B．
3
2
C．
2
3
D．
18
组卷：282引用：4难度：0.7
解析
4．
（
-
4
）
2
的值为（　　）
A．4 B．±4 C．2 D．±2
组卷：29引用：7难度：0.9
解析
5．下列调查中，适宜采用普查方式的是（　　）
A．了解一批圆珠笔的寿命
B．了解全国九年级学生身高的现状
C．检查神舟号载人飞船的各零部件
D．考查人们保护海洋的意识
组卷：106引用：3难度：0.9
解析
6．若关于x的分式方程
2
x
-
1
=
m
x
有正整数解，则整数m的值是（　　）
A．3 B．5 C．3或5 D．3或4
组卷：2367引用：14难度：0.7
解析
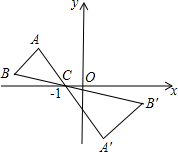7．如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（-1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，记所得的像是△A′B′C．设点B的对应点B′的横坐标是a,则点B的横坐标是（　　）
A．
-
1
2
a
B．
-
1
2
（
a
+
1
）
C．
-
1
2
（
a
-
1
）
D．
-
1
2
（
a
+
3
）
组卷：1792引用：58难度：0.5
解析
8．若一次函数y=ax+b与反比例函数y=
c
x
的图象在第二象限内有两个交点，且其中一个交点的横坐标为-1，则二次函数y=ax²+bx-c的图象可能是（　　）
A． B． C． D．
组卷：876引用：14难度：0.6
解析

二.填空题（共10小题，满分30分，每小题3分）

9．代数式
x
x
+
2
在实数范围内有意义，则实数x的取值范围是
．
组卷：116引用：3难度：0.7
解析

当前模式为游客模式，立即登录查看试卷全部内容及下载

三.解答题（共10小题，满分96分）

27．我们定义：若一个三角形最大边上的点将该边分为两条线段，且这两条线段的积等于这个点到最大边所对顶点连线的平方，则称这个点为这个三角形的“比例中点”．例如：如图1，已知钝角△ABC中，∠ACB是钝角，点D是AB上的一点，连接CD，若CD²=AD•BD，则称点D是△ABC的“比例中点”．

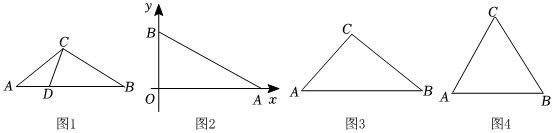
（1）如图2，已知点A的坐标为（4，0），点B在y轴上，∠BAO=30°，若点M是△AOB的“比例中点”，则点M的坐标为
；
（2）如图3，已知△ABC中，AB=28，∠A=45°，
tan
B
=
3
4
，若点N是△ABC的“比例中点”，求AN；
（3）如图4，已知△ABC是等边三角形，因为等边三角形的三边相等，所以其中任意一条边都可以看成最大边，试判断等边三角形有没有“比例中点”？说明理由．
组卷：506引用：4难度：0.1
解析
28．如图，二次函数y=
1
2
x²+bx+c与x轴交于O（0，0），A（4，0）两点，顶点为C，连接OC、AC，若点B是线段OA上一动点，连接BC，将△ABC沿BC折叠后，点A落在点A′的位置，线段A′C与x轴交于点D，且点D与O、A点不重合．
（1）求二次函数的表达式；
（2）①求证：△OCD∽△A′BD；
②求
DB
BA
的最小值；
（3）当S_△OCD=8S_△A'BD时，求直线A′B与二次函数的交点横坐标．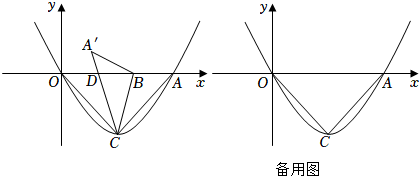
组卷：3702引用：9难度：0.1
解析