2022-2023学年江西省宜春市宜丰中学创新部九年级（上）开学数学试卷

一、单选题（3*6=18分）

• 1．下面四幅图是我国一些博物馆的标志，其中既是轴对称图形又是中心对称图形的是（　　）

  A． 温州博物馆

  B． 西藏博物馆

  C． 广东博物馆

  D． 湖北博物馆
  组卷：663引用：16难度：0.9

  解析

• 2．关于x的方程

  （

  a

  +

  2

  ）

  x

  a

  2

  -

  2

  -

  3

  x

  -

  1

  =

  0

  是一元二次方程，则a的值是（　　）

  A．a=±2

  B．a=-2

  C．a=2

  D． a =± 2
  组卷：322引用：16难度：0.9

  解析

• 3．一个不透明的盒子里装有除颜色外完全相同的球，其中有6个白球m个篮球，每次将球充分搅匀后，任意摸出1个球记下颜色然后再放回盒子里，通过如此大量重复试验，发现摸到白球的频率稳定在0.4左右，则m的值约为（　　）

  A．4

  B．6

  C．9

  D．12
  组卷：17引用：3难度：0.5

  解析

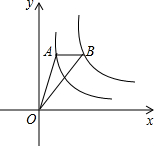• 4．如图，点A是反比例函数y₁=

  1

  x

  （x＞0）图象上一点，过点A作x轴的平行线，交反比例函数

  y

  2

  =

  k

  x

  （x＞0）的图象于点B，连接OA、OB，若△OAB的面积为1，则k的值是（　　）

  A．3

  B．4

  C．5

  D．6
  组卷：117引用：3难度：0.6

  解析

• 5．如图，在△ABC中，∠ABC=Rt∠，AB=4，BC=3，D是AB的中点，DE⊥AC交AC于点E，则AE的长是（　　）

  A． 6 5

  B． 8 5

  C． 5 3

  D．1
  组卷：61引用：4难度：0.6

  解析

• 6．小明将直径为6cm的半圆绕点A逆时针旋转60°设计了如图所示的图案，那么图中阴影部分的面积是（　　）

  A．4.5πcm2

  B．6πcm2

  C．9πcm2

  D．18πcm2
  组卷：122引用：3难度：0.4

  解析

二、填空题（3*6=18分）

• 7．已知扇形的圆心角的度数是120˚，半径为9，则此扇形弧长是

  ．
  组卷：68引用：4难度：0.9

  解析

三、解答题

• 21．如图1，锐角△ABD（AB＜AD）内接于⊙M，弦AC⊥BD于点O．已知⊙M半径为5，且AC=BD．
  （1）求∠ADB的度数；
  （2）若△ABO的面积为

  7

  2

  ，求BD的长；
  （3）如图2，在（2）的条件下，点E，F分别在OD，MD上，连接EF，ME，若∠DEF=∠DAB，求△MEF面积的最大值．
  
  组卷：279引用：4难度：0.3

  解析

• 22．我们知道，平面内互相垂直且有公共原点的两条数轴构成平面直角坐标系，如果两条数轴不垂直，而是相交成任意的角ω（0°＜ω＜180°且ω≠90°），那么这两条数轴构成的是平面斜坐标系，两条数轴称为斜坐标系的坐标轴，公共原点称为斜坐标系的原点，如图1，经过平面内一点P作坐标轴的平行线PM和PN，分别交x轴和y轴于点M，N．点M、N在x轴和y轴上所对应的数分别叫做P点的x坐标和y坐标，有序实数对（x,y）称为点P的斜坐标，记为P（x,y）．
  
  （1）如图2，ω=45°，矩形OABC中的一边OA在x轴上，BC与y轴交于点D，OA=2，OC=1．
  ①点A、B在此斜坐标系内的坐标分别为A

  、B

  ；
  ②设点P（x,y）在经过O、B两点的直线上，直接写出y与x之间满足的关系为

  ；
  （2）若ω=120°，O为坐标原点．
  ①如图3，圆M与y轴相切原点O，被x轴截得的弦长OA=

  4

  3

  ，求圆心M的斜坐标；
  ②如图4，圆M的圆心斜坐标为M（2，2），若圆上恰有两个点到y轴的距离为1，则圆M的半径r的取值范围．
  组卷：33引用：1难度：0.1

  解析