2023-2024学年江苏省南京市秦淮外国语学校八年级（上）月考数学试卷（10月份）

一.选择题（每题2分，共16分）

• 1．下列图形中，不是轴对称图形的是（　　）

  A．

  B．

  C．

  D．
  组卷：102引用：11难度：0.9

  解析

• 2．如图，已知BF=DE，AB∥CD，要使△ABF≌△CDE，添加的条件可以是（　　）

  A．BE=DF

  B．AF=CE

  C．AF∥CE

  D．∠B=∠D
  组卷：990引用：8难度：0.7

  解析

• 3．如图，在△ABC中，AB的垂直平分线分别交AB，BC于点D，E，AC的垂直平分线分别交AC，BC于点F，G，且△AEG的周长是20，则线段BC的长为（　　）

  A．40

  B．20

  C．15

  D．10
  组卷：1074引用：4难度：0.7

  解析

• 4．某地兴建的幸福小区的三个出口A、B、C的位置如图所示，物业公司计划在不妨碍小区规划的建设下，想在小区内修建一个电动车充电桩，以方便业主，要求到三个出口的距离都相等，则充电桩应该在△ABC（　　）

  A．三条高线的交点处

  B．三条中线的交点处

  C．三个角的平分线的交点处

  D．三条边的垂直平分线的交点处
  组卷：2389引用：44难度：0.7

  解析

• 5．如图，∠ACD=120°，AB=BC=CD，则∠A等于（　　）
  

  A．10°

  B．15°

  C．20°

  D．30°
  组卷：603引用：4难度：0.7

  解析

• 6．如图，已知△ABC的面积为48，AB=AC=6，点D为BC边上一点，过点D分别作DE⊥AB于E，DF⊥AC于F，若DF=3DE，则DF长为（　　）

  A．12

  B．10

  C．6

  D．8
  组卷：441引用：3难度：0.7

  解析

• 7．等腰三角形一腰上的高与另一腰所成的夹角为45°，则顶角的度数为（　　）

  A．45°或135°

  B．45°

  C．135°

  D．90°
  组卷：629引用：6难度：0.9

  解析

• 8．如图，∠MON=α，α＜30°，点A为ON上一定点，点C为ON上一动点，B，D为OM上两动点，当AB+BC+CD最小时，∠BCD+∠ABC=（　　）

  A．5α

  B．6α

  C．90°-α

  D．180°-α
  组卷：2844引用：4难度：0.4

  解析

三、解答题（共64分）

• 25．如图1，BE是△ABC中AC边上的高，点D是AB上一点，连接CD交BE于点F，∠EFC=∠A．
  （1）求证：CD⊥AB；
  （2）若∠ACB=2∠ABE，求证：AC=BC；
  （3）如图2，在（2）的条件下，延长BE至点G，连接AG，CG，若S_{四边形ABCG}=

  B

  C

  2

  2

  ，S_△ABG=25，求线段AB的长．
  
  组卷：214引用：2难度：0.1

  解析

• 26．我们知道：过三角形的顶点引一条直线，可以将它分割成两个小三角形．如果每个小三角形都有两个相等的内角，则我们称这条直线为原三角形的“美丽线”．如图1，直线CD为△ABC的“美丽线”．
  
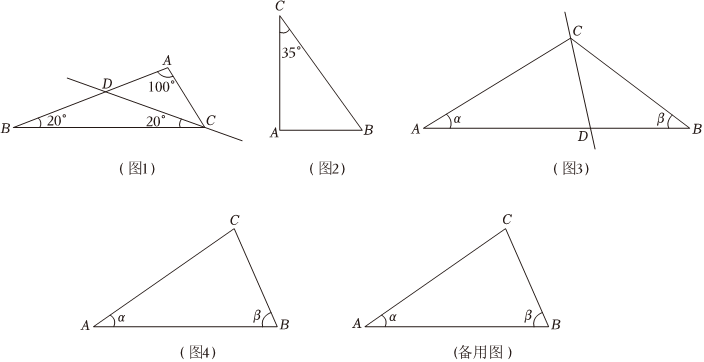
  （1）如图2，在△ABC中，∠A=90°，∠C=35°，请利用直尺和量角器在图2中画出△ABC的“美丽线”（标出所得三角形的内角度数，不要求写画法）；
  （2）在△ABC中，∠A=α，∠B=β（α≤β）．若△ABC存在过点C的“美丽线”，试探究α与β的关系．下面是对这个问题的部分探究过程：
  设CD为△ABC的“美丽线”，点D在边AB上，则△ACD与△BCD中各有两个相等的内角．
  【探究1】
  如图3，当∠ACD=∠ADC时，因为∠A=α，所以∠ADC=

  ，且∠ADC为锐角，则∠CDB为钝角，所以在△CDB 中，∠DCB=∠B=β．由此可以得到α与β的关系为

  ，其中α的取值范围为

  ．
  【探究2】
  借助图4，请你继续完成本问题的探究，直接写出α与β的关系．
  组卷：1274引用：8难度：0.5

  解析