我们知道：过三角形的顶点引一条直线，可以将它分割成两个小三角形．如果每个小三角形都有两个相等的内角，则我们称这条直线为原三角形的“美丽线”．如图1，直线CD为△ABC的“美丽线”．
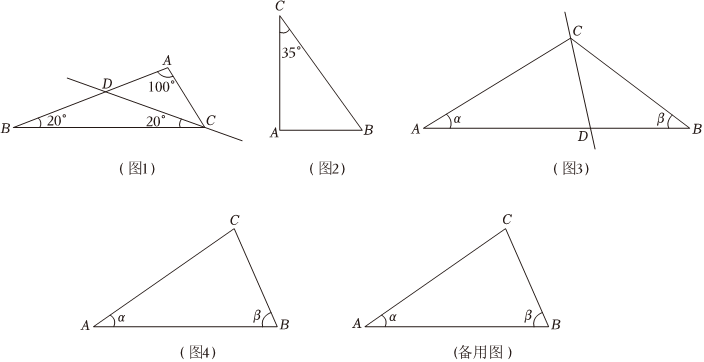
（1）如图2，在△ABC中，∠A=90°，∠C=35°，请利用直尺和量角器在图2中画出△ABC的“美丽线”（标出所得三角形的内角度数，不要求写画法）；
（2）在△ABC中，∠A=α，∠B=β（α≤β）．若△ABC存在过点C的“美丽线”，试探究α与β的关系．下面是对这个问题的部分探究过程：
设CD为△ABC的“美丽线”，点D在边AB上，则△ACD与△BCD中各有两个相等的内角．
【探究1】
如图3，当∠ACD=∠ADC时，因为∠A=α，所以∠ADC=180°-α2180°-α2，且∠ADC为锐角，则∠CDB为钝角，所以在△CDB 中，∠DCB=∠B=β．由此可以得到α与β的关系为 α=180°-4βα=180°-4β，其中α的取值范围为 0°＜α≤36°0°＜α≤36°．
【探究2】
借助图4，请你继续完成本问题的探究，直接写出α与β的关系．
180
°
-
α
2
180
°
-
α
2
【考点】三角形综合题．
【答案】；α=180°-4β；0°＜α≤36°
180
°
-
α
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/29 8:0:9组卷：1283引用：8难度：0.5
相似题
-
1．如图1，已知，在Rt△ABC中，∠C=90°，AC=4，BC=3，点D在AB上且
，点P，Q分别从点D，B出发沿线段DB，BC向终点B，C匀速移动，P，Q两点同时出发，同时到达终点．设BQ=x,AP=y.BD=154
（1）求AD的值．
（2）求y关于x的函数表达式．
（3）如图2，过点P作PE⊥AC于点E，连结PQ，EQ．
①当△PEQ为等腰三角形时，求x的值．
②过D作DF⊥BC于点F，作点F关于EQ的对称点F'，当点F'落在△PQB的内部（不包括边界）时，则x的取值范围为 ．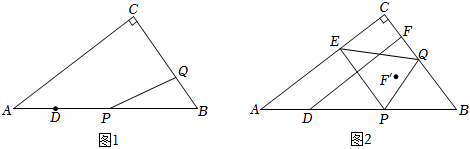
发布：2025/6/13 1:30:1组卷：84引用：3难度：0.1 -
2．在等腰△ABC中，AB=AC，∠BAC=120°，D、E、F分别为线段BC、AB、AC上的点，∠AEF=∠CAD，AD交EF于点G．
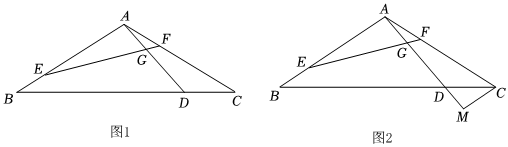
（1）如图1，求∠AGE的度数；
（2）如图2，已知BE=AF，点M在AD的延长线上，AM=EF，连接CM．
①求证：CM∥AB；②若，直接写出ADEF=45的值为 ．CMAB发布：2025/6/13 1:30:1组卷：64引用：2难度：0.1 -
3．如图1，在△ABC中，AB=AC，D、E在BC边上，连接AD、AE，AD=AE．
（1）若∠B=30°，∠DAE=40°，则∠BAD=°；
（2）如图2，∠BAE+∠C=90°+∠ADE，F为AE上一点，连接DF、CF，且AF=CE，M为DF中点，连接AM，证明∠DAM=∠BAD．12
（3）如图3，∠DAE=60°，DE=a,F为AE的中点，连接DF，DF=b,点M在DF上，连接AM，在AM的右侧作等边△AMN，连接NF，请直接写出△ANF周长的最小值．
发布：2025/6/13 1:0:1组卷：448引用：5难度：0.3
