2022-2023学年北京市通州区高一（下）期末数学试卷

一、选择题共10小题，每小题4分，共40分。在每小题列出的四个选项中，选出符合题目要求的

• 1．已知P是复平面内表示复数a+bi（a,b∈R）的点，若复数a+bi是虚数，则点P（　　）

  A．在虚轴上

  B．不在虚轴上

  C．在实轴上

  D．不在实轴上
  组卷：66引用：1难度：0.7

  解析

• 2．对于任意两个向量

  a

  和

  b

  ，下列命题中正确的是（　　）

  A．| a + b |≤| a - b |

  B．| a - b |≤| a + b |

  C．| a + b |≤| a |+| b |

  D．| a - b |≤|| a |-| b ||
  组卷：266引用：1难度：0.7

  解析

• 3．在△ABC中，若2acosB=c,则△ABC一定是（　　）

  A．等腰三角形	B．直角三角形
  C．等腰直角三角形	D．等边三角形
  组卷：80引用：1难度：0.7

  解析

• 4．从甲、乙、丙、丁四人中随机选取两人，则甲被选中的概率为（　　）

  A． 1 4

  B． 1 3

  C． 1 2

  D． 3 4
  组卷：129引用：2难度：0.7

  解析

• 5．已知一组数据有40个，把它分成六组，第一组到第四组的频数分别为10，5，7，6，第五组的频率是0.20，则第六组的频率是（　　）

  A．0.10

  B．0.12

  C．0.15

  D．0.18
  组卷：88引用：2难度：0.7

  解析

• 6．某市6月前10天的空气质量指数为35，54，80，86，72，85，58，125，111，58，则这组数据的第70百分位数是（　　）

  A．86

  B．85.5

  C．85

  D．84.5
  组卷：115引用：2难度：0.7

  解析

• 7．下列命题正确的是（　　）

  A．一条线段和不在这条线段上的一点确定一个平面

  B．两条不平行的直线确定一个平面

  C．三角形上不同的三个点确定一个平面

  D．圆上不同的三个点确定一个平面
  组卷：40引用：1难度：0.5

  解析

三、解答题共6小题，共85分。解答应写出文字说明，演算步骤或证明过程。

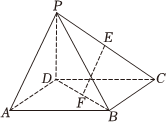• 20．如图，在四棱锥P-ABCD中，底面ABCD是矩形，PD⊥底面ABCD，且PD=1，

  AB

  =

  3

  ，AD=2，E，F分别是PC，BD的中点．
  （Ⅰ）求证：EF∥平面PAD；
  （Ⅱ）再从条件①、条件②、条件③这三个条件中选择一个作为已知，求三棱锥G-DCE的体积．
  条件①：G是棱BC上一点，且BG=2GC；
  条件②：G是PB的中点；
  条件③：G是△PBC的内心（内切圆圆心）．
  组卷：154引用：1难度：0.5

  解析

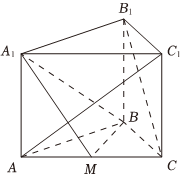• 21．如图，在直三棱柱ABC-A₁B₁C₁ 中，点M在棱AC上，且B₁C∥平面A₁BM，AB=BC，AC=2，

  A

  A

  1

  =

  2

  ．
  （Ⅰ）求证：M是棱AC的中点；
  （Ⅱ）求证：AC₁⊥平面A₁BM，
  （Ⅲ）在棱BB₁上是否存在点N，使得平面AC₁N⊥平面ACC₁A₁？如果存在，求出

  BN

  B

  B

  1

  的值；如果不存在，请说明理由．
  组卷：344引用：1难度：0.5

  解析