2022-2023学年山西省大同六中八年级（上）期中数学试卷
发布：2024/9/8 2:0:8
一、选择题（本大题共10个小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项符合题目要求）
-
1．平面直角坐标系中，P（3，-2），则点P关于y轴对称的点的坐标为（ ）
组卷：116引用：8难度：0.7 -
2．已知一个三角形的两边长分别为8和2，则这个三角形的第三边长可能是（ ）
组卷：1465引用：14难度：0.6 -
3．下列四个图案中，不是轴对称图案的是（ ）
组卷：60引用：5难度：0.9 -
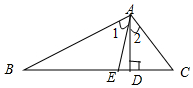4．如图，在△ABC中，AD⊥BC，AE平分∠BAC，若∠1=30°，∠2=20°，则∠B=（ ）组卷：892引用：5难度：0.8 -
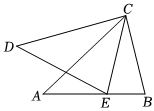5．如图，△ABC≌△DEC，其中AC和DC是对应边，CB和CE是对应边，点E在线段AB上．若∠AED+∠BCE=54°，则∠AED的度数为（ ）组卷：14引用：1难度：0.7 -
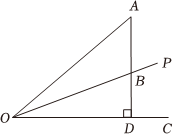6．如图所示，OP是∠AOC的平分线，点B在OP上，AB⊥OC于点D，∠A=45°．若OD=2+2，点B到OA的距离为2，则AB长为（ ）2组卷：17引用：3难度：0.5 -
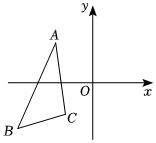7．如图，在平面直角坐标系中，将△ABC的三个顶点坐标的横坐标都乘-1，并保持纵坐标不变，画出对应的△A′B′C′，则△A′B′C′和△ABC的关系是（ ）组卷：18引用：1难度：0.8
三、解答题（本大题共8个小题，共75分．解答应写出文字说明、证明过程或演算步骤）
-
22．综合与实践：
问题情境：
已知在△ABC中，∠BAC=100°，∠ABC=∠ACB，点D为直线BC上的动点（不与点B，C重合），点E在直线AC上，且AE=AD，设∠DAC=n.
（1）如图1，若点D在BC边上，当n=36°时，求∠BAD和∠CDE的度数；
拓广探索：
（2）如图2，当点D运动到点B的左侧时，其他条件不变，试猜想∠BAD和∠CDE的数量关系，并说明理由；
（3）当点D运动点C的右侧时，其他条件不变，请直接写出∠BAD和∠CDE的数量关系．
组卷：1858引用：5难度：0.5 -
23．综合与实践．
积累经验
（1）我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在△ABC中，∠ACB=90°，AC=BC，线段DE经过点C，且AD⊥DE于点D，BE⊥DE于点E．求证：AD=CE，CD=BE”这个问题时，只要证明△ADC≌△CEB，即可得到解决，请写出证明过程；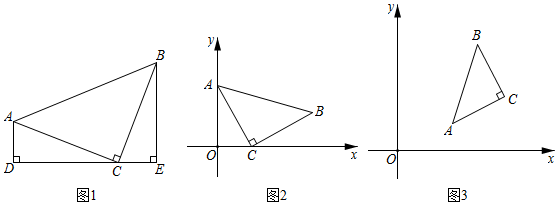
类比应用
（2）如图2，在平面直角坐标系中，△ABC中，∠ACB=90°，AC=BC，点A的坐标为（0，2），点C的坐标为（1，0），求点B的坐标．
拓展提升
（3）如图3，△ABC在平面直角坐标系中，∠ACB=90°，AC=BC，点A的坐标为（2，1），点C的坐标为（4，2），则点B的坐标为 ．组卷：629引用：10难度：0.4
