综合与实践．
积累经验
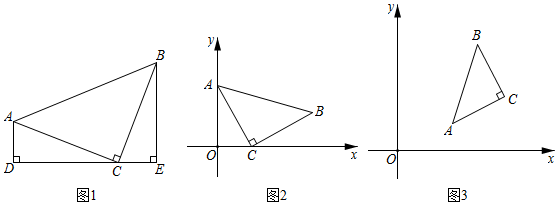
（1）我们在第十二章《全等三角形》中学习了全等三角形的性质和判定，在一些探究题中经常用以上知识转化角和边，进而解决问题．例如：我们在解决：“如图1，在△ABC中，∠ACB=90°，AC=BC，线段DE经过点C，且AD⊥DE于点D，BE⊥DE于点E．求证：AD=CE，CD=BE”这个问题时，只要证明△ADC≌△CEB，即可得到解决，请写出证明过程；
类比应用
（2）如图2，在平面直角坐标系中，△ABC中，∠ACB=90°，AC=BC，点A的坐标为（0，2），点C的坐标为（1，0），求点B的坐标．
拓展提升
（3）如图3，△ABC在平面直角坐标系中，∠ACB=90°，AC=BC，点A的坐标为（2，1），点C的坐标为（4，2），则点B的坐标为 （3，4）（3，4）．
【考点】三角形综合题．
【答案】（3，4）
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/31 14:0:8组卷：629引用：10难度：0.4
相似题
-
1．如图1，已知点B（0，9），点C为x轴上一动点，连接BC，△ODC和△EBC都是等边三角形．
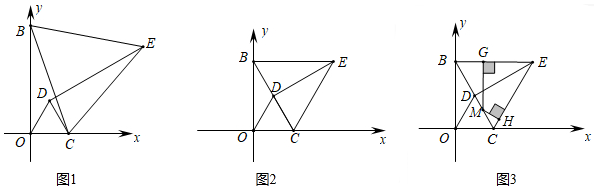
（1）求证：DE=BO；
（2）如图2，当点D恰好落在BC上时．
①求点E的坐标；
②在x轴上是否存在点P，使△PEC为等腰三角形？若存在，写出点P的坐标；若不存在，说明理由；
③如图3，点M是线段BC上的动点（点B，点C除外），过点M作MG⊥BE于点G，MH⊥CE于点H，当点M运动时，MH+MG的值是否发生变化？若不会变化，直接写出MH+MG的值；若会变化，简要说明理由．发布：2025/6/13 6:0:2组卷：1705引用：7难度：0.1 -
2．【阅读】
定义：如果一个三角形有两个内角的差为90°，那么这样的三角形叫做“准直角三角形”．
【理解】
（1）①若∠A=60°，∠B=15°，则△ABC “准直角三角形”；（填“是”或“不是”）
②已知△ABC是“准直角三角形”，且∠C＞90°，∠A=40°，则∠B的度数为 ．
【应用】
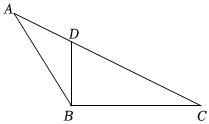
（2）如图，在△ABC中，点D在AC上，连接BD．若BD=AD，AC=18，BC=12，AD：CD=5：13，试说明△ABC是“准直角三角形”．发布：2025/6/13 7:0:2组卷：164引用：4难度：0.3 -
3．小明遇到这样一个问题：△ABC是等边三角形，点D在射线BC上，且满足∠ADE=60°，DE交等边△ABC外角平分线CE于点E，试探究AD与DE的数量关系．
（1）（初步探究）
小明发现，当点D为BC的中点时，如图①，过点D作DF∥AC，交AB于点F，通过构造全等三角形，经过推理论证，能够得到线段AD与DE的数量关系，请直接写出结论；
（2）（类比探究）
当点D是线段BC上（不与点B，C重合）任意一点时，其他条件不变，如图②，试猜想AD与DE之间的数量关系，并证明你的结论；
（3）（拓展应用）
当点D在BC的延长线上时，满足CD=BC，其他条件不变，连接AE，请在图③中补全图形，并直接写出∠AED的大小．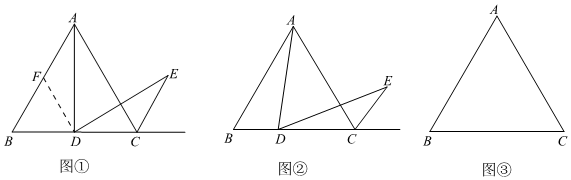
发布：2025/6/13 5:30:2组卷：239引用：2难度：0.1
